题目内容
在正项等比数列{an}中,已知a3a5=64,则a1+a7的最小值为( )
| A.64 | B.32 | C.16 | D.8 |
∵数列{an}是等比数列,且a3•a5=64,
由等比数列的性质得:a1a7=a3a5=64,
∴a1+a7≥2
=2
=16..
∴a1+a7的最小值是16.
故选:C.
由等比数列的性质得:a1a7=a3a5=64,
∴a1+a7≥2
| a1a7 |
| 64 |
∴a1+a7的最小值是16.
故选:C.

练习册系列答案
相关题目
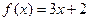 ,数列
,数列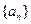 满足:
满足: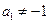 且
且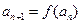 (nÎN*),若数列
(nÎN*),若数列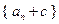 是等比数列,则常数c = .
是等比数列,则常数c = .