题目内容
已知抛物线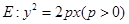 的准线与x轴交于点M,过点M作圆
的准线与x轴交于点M,过点M作圆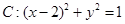 的两条切线,切点为A、B,
的两条切线,切点为A、B,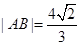 .
.
(1)求抛物线E的方程;
(2)过抛物线E上的点N作圆C的两条切线,切点分别为P、Q,若P,Q,O(O为原点)三点共线,求点N的坐标.
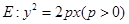 的准线与x轴交于点M,过点M作圆
的准线与x轴交于点M,过点M作圆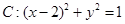 的两条切线,切点为A、B,
的两条切线,切点为A、B,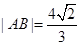 .
.(1)求抛物线E的方程;
(2)过抛物线E上的点N作圆C的两条切线,切点分别为P、Q,若P,Q,O(O为原点)三点共线,求点N的坐标.
(1)y2=4x;(2)点N坐标为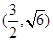 或
或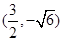 .
.
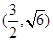 或
或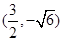 .
.试题分析:本题主要考查抛物线的标准方程及其几何性质、圆的标准方程及其几何性质、圆的切线的性质等基础知识,考查学生分析问题解决问题的能力和计算能力.第一问,利用抛物线的准线,得到M点的坐标,利用圆的方程得到圆心C的坐标,在
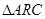 中,可求出
中,可求出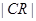 ,在
,在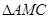 中,利用相似三角形进行角的转换,得到
中,利用相似三角形进行角的转换,得到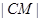 的长,而
的长,而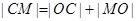 ,从而解出P的值,即得到抛物线的标准方程;第二问,设出N点的坐标,利用N、C点坐标写出圆C的方程,利用点C的坐标写出圆C的方程,两方程联立,由于P、Q是两圆的公共点,所以联立得到的方程即为直线PQ的方程,而O点在直线上,代入点O的坐标,即可得到s、t的值,即得到N点坐标.
,从而解出P的值,即得到抛物线的标准方程;第二问,设出N点的坐标,利用N、C点坐标写出圆C的方程,利用点C的坐标写出圆C的方程,两方程联立,由于P、Q是两圆的公共点,所以联立得到的方程即为直线PQ的方程,而O点在直线上,代入点O的坐标,即可得到s、t的值,即得到N点坐标.试题解析:(1)由已知得
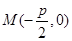 ,C(2,0).
,C(2,0).设AB与x轴交于点R,由圆的对称性可知,
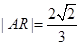 .
.于是
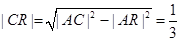 ,
,所以
 ,即
,即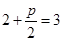 ,p=2.
,p=2.故抛物线E的方程为y2=4x. 5分
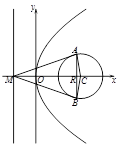
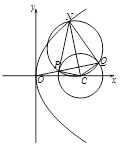
(2)设N(s,t).
P,Q是NC为直径的圆D与圆C的两交点.
圆D方程为
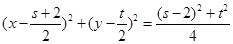 ,
,即x2+y2-(s+2)x-ty+2s=0. ①
又圆C方程为x2+y2-4x+3=0. ②
②-①得(s-2)x+ty+3-2s=0. ③ 9分
P,Q两点坐标是方程①和②的解,也是方程③的解,从而③为直线PQ的方程.
因为直线PQ经过点O,所以3-2s=0,
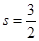 .
.故点N坐标为
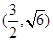 或
或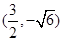 . 12分
. 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 面积的最小值.
面积的最小值. ,4),则|PA|+|PM|的最小值是
,4),则|PA|+|PM|的最小值是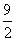
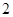 米时,量得水面宽为
米时,量得水面宽为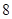 米.则水面升高
米.则水面升高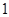 米后,水面
米后,水面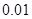 米).
米).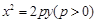 ,过点
,过点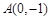 作直线
作直线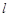 与抛物线相交于
与抛物线相交于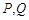 两点,点
两点,点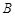 的坐标为
的坐标为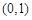 ,连接
,连接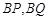 ,设
,设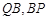 与
与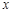 轴分别相交于
轴分别相交于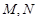 两点.如果
两点.如果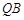 的斜率与
的斜率与 的斜率的乘积为
的斜率的乘积为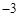 ,则
,则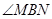 的大小等于.
的大小等于.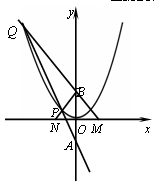
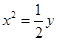 的焦点到准线的距离是( )
的焦点到准线的距离是( )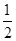
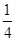
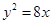 的准线方程是 .
的准线方程是 .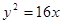 的准线为( )
的准线为( ) 的焦点坐标是_____________.
的焦点坐标是_____________.