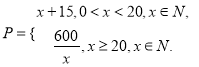Question

【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.

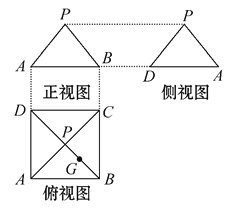
(1)根据三视图,画出该几何体的直观图.

(2)在直观图中,①证明:PD∥平面AGC;

②证明:平面PBD⊥平面AGC.

Answer 1

【答案】（1）见解析；（2）见解析

【解析】试题分析：（1）根据三视图，可得该几何体为正四棱锥，正方形的边长为2，正四棱锥的高为，由此可得该几何体的直观图．
（Ⅱ）①在直观图中，设正方形的中心为，利用三角形的中位线证明 ．再由直线和平面平行的判定定理证得面．
②连接，则，取的中点，连接 ，则 ，即可求此几何体的侧面积．

试题解析：(1)该几何体的直观图如图所示.

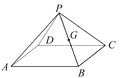
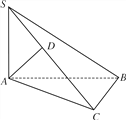
(2)如图,①连接AC,BD交于点O,连接OG,

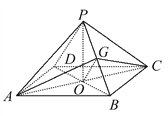
因为G为PB的中点,O为BD的中点,所以OG∥PD，又OG平面AGC,PD平面AGC,所以PD∥平面AGC.

②连接PO,由三视图,PO⊥平面ABCD,所以AO⊥PO.又AO⊥BO,BO∩PO=O,所以AO⊥平面PBD，因为AO平面AGC,所以平面PBD⊥平面AGC.