题目内容
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101﹣150为轻度污染;151﹣200为中度污染;201~300为重度污染;>300为严重污染. 一环保人士记录去年某地某月10天的AQI的茎叶图如图.
(Ⅰ)利用该样本估计该地本月空气质量优良(AQI≤100)的天数;(按这个月总共30天)
(Ⅱ)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为ξ,求ξ的概率分布列和数学期望.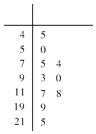
【答案】解:(Ⅰ)从茎叶图中可以发现这样本中空气质量优的天数为2, 空气质量良的天数为4,
∴该样本中空气质量优良的频率为 ![]() ,
,
从而估计该月空气质量优良的天数为30× ![]() =18.
=18.
(Ⅱ)由(1)估计某天空气质量优良的概率为 ![]() ,ξ的所有可能取值为0,1,2,3,
,ξ的所有可能取值为0,1,2,3,
且ξ~B(3, ![]() ),
),
P(ξ=0)=( ![]() )3=
)3= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)=( ![]() )3=
)3= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴Eξ=3× ![]() =1.8.
=1.8.
【解析】(1)从茎叶图中可以发现这样本中空气质量优的天数为2,空气质量良的天数为4,由此能求出该样本中空气质量优良的频率,从而能估计该月空气质量优良的天数.(2)估计某天空气质量优良的概率为 ![]() ,ξ的所有可能取值为0,1,2,3,且ξ~B(3,
,ξ的所有可能取值为0,1,2,3,且ξ~B(3, ![]() ),由此能求出ξ的概率分布列和数学期望.
),由此能求出ξ的概率分布列和数学期望.
【考点精析】利用茎叶图和离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案