题目内容
【题目】如图，AB是⊙O的直径，C是圆周上不同于A，B的任意一点，PA⊥平面ABC，则四面体P-ABC的四个面中，直角三角形的个数有（ ）
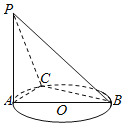
A. 4个B. 3个C. 2个D. 1个
【答案】A
【解析】
由题意得出三角形ABC是直角三角形，根据线面垂直的性质定理得出PA垂直于AC，BC，从而得出两个直角三角形，又可证明BC垂直于平面PAC，从而得出三角形PBC也是直角三角形，从而问题解决．
∵AB是圆O的直径
∴∠ACB＝90°即BC⊥AC，三角形ABC是直角三角形
又∵PA⊥圆O所在平面，
∴△PAC，△PAB是直角三角形．
且BC在这个平面内，
∴PA⊥BC 因此BC垂直于平面PAC中两条相交直线，
∴BC⊥平面PAC，
∴△PBC是直角三角形．
从而△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是：4．
故选：A．
练习册系列答案
相关题目
【题目】某校在本校任选了一个班级，对全班50名学生进行了作业量的调查，根据调查结果统计后，得到如下的
列联表，已知在这50人中随机抽取2人，这2人都“认为作业量大”的概率为
.
| 认为作业量大 | 认为作业量不大 | 合计 |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
（Ⅰ）请完成上面的列联表；
（Ⅱ）根据列联表的数据，能否有
的把握认为“认为作业量大”与“性别”有关？
（Ⅲ）若视频率为概率，在全校随机抽取4人，其中“认为作业量大”的人数记为
，求的分布列及数学期望.
附表：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附：
