题目内容
6．已知△ABC中，C=2B，若∠BAC的平分线把△ABC的面积分成$\sqrt{3}$：1两部分，则A=90°．分析 如图，AD是∠BAC的平分线．由两三角形的面积比为$\sqrt{3}$：1可得相应的边长之比，利用正弦定理可得正弦之比，然后转化为角B的关系式，由特殊角的三角函数值得到B=30°，则C=60°，由三角形内角和定理得到A的度数．
解答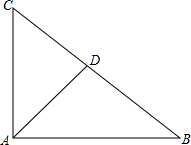 
解：由题意可得，S△ABD：S△ACD=$\sqrt{3}$：1，BD：CD=$\sqrt{3}$：1，
由正弦定理得，$\frac{AD}{sinC}$=$\frac{CD}{sin\frac{A}{2}}$，$\frac{AD}{sinB}$=$\frac{BD}{sin\frac{A}{2}}$，
所以$\frac{sinC}{sinB}$=$\frac{BD}{CD}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$，即$\frac{2sinBcosB}{sinB}$=$\sqrt{3}$，
所以cosB=$\frac{\sqrt{3}}{2}$，
因为0＜B＜π，
所以B=30°，
所以C=2B=60°
所以A=90°，
故答案为：90°．
点评 本题考查正弦定理的应用、三角函数中的恒等变换，考查学生分析解决问题的能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．若方程$\frac{2}{x}$+ln$\frac{1}{x-1}$=0的解为x0，则x0所在的大致区间是（ ）
| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （5，6） |
14．阅读如图所示的算法框图，运行相应的程序，则循环体执行的次数是（ ）
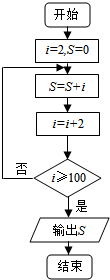
| A． | 50 | B． | 49 | C． | 100 | D． | 98 |
1．函数$y=sin（-3x+\frac{π}{4}）$的最小正周期是（ ）
| A． | $\frac{2π}{3}$ | B． | $-\frac{2π}{3}$ | C． | $\frac{π}{3}$ | D． | $-\frac{π}{3}$ |
11．函数y=$\frac{1}{3}$x3-x2+5在x=1处的切线倾斜角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{3π}{4}$ |
18．${∫}_{0}^{1}$（ex+2x）dx等于（ ）
| A． | 1 | B． | e-1 | C． | e | D． | e+1 |
15．cos15°的值为（ ）
| A． | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B． | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | C． | $2-\sqrt{3}$ | D． | $2+\sqrt{3}$ |
16．
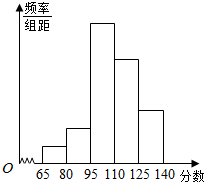为了解某校高三学生质检数学成绩分布，从该校参加质检的学生数学成绩中抽取一个样本，并分成5组，绘成如图所示的频率分布直方图．若第一组至第五组数据的频率之比为1：2：8：6：3，最后一组数据的频数是6．用频率估计概率的方法，估计该校高三学生质检数学成绩在125～140分之间的概率和样本容量为（ ）
为了解某校高三学生质检数学成绩分布，从该校参加质检的学生数学成绩中抽取一个样本，并分成5组，绘成如图所示的频率分布直方图．若第一组至第五组数据的频率之比为1：2：8：6：3，最后一组数据的频数是6．用频率估计概率的方法，估计该校高三学生质检数学成绩在125～140分之间的概率和样本容量为（ ）| A． | $\frac{1}{10}$，60 | B． | $\frac{2}{5}$，15 | C． | $\frac{3}{10}$，20 | D． | $\frac{3}{20}$，40 |