题目内容
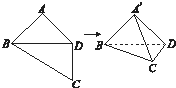如图，四边形ABCD中，AB=AD=CD=1，BD=| 2 |
考点：平面与平面垂直的性质
专题：空间位置关系与距离
分析：由已知得BA′⊥A′D，CD⊥平面A'BD，从而BA′⊥CD，进而BA′⊥平面A′CD，由此能求出∠BA′C=90°．
解答：解：∵A′B=A′D=1，BD=
，∴A′B2+A′D2=BD2
∴BA′⊥A′D
∵平面A'BD⊥平面BCD，BD⊥CD，
平面A'BD∩平面BCD=BD
∴CD⊥平面A'BD
∵BA′?平面A'BD
∴BA′⊥CD
∵A′D∩CD=D
∴BA′⊥平面A′CD，
∴∠BA′C=90°．
故答案为：90°．
| 2 |
∴BA′⊥A′D
∵平面A'BD⊥平面BCD，BD⊥CD，
平面A'BD∩平面BCD=BD
∴CD⊥平面A'BD
∵BA′?平面A'BD
∴BA′⊥CD
∵A′D∩CD=D
∴BA′⊥平面A′CD，
∴∠BA′C=90°．
故答案为：90°．
点评：本题考查角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
已知函数f（x）=
，若f（a）=1，则a的所有可能结果之和为（ ）
|
| A、e | ||
B、
| ||
C、e+
| ||
D、2e+
|
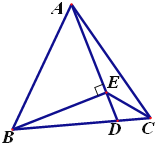如图，△ABC是边长为2的等边三角形，D是边BC上的动点，BE⊥AD于E，则CE的最小值为（ ）| A、1 | ||||
B、2-
| ||||
C、
| ||||
D、
|
正四棱锥S-ABCD中，SA=AB，则直线AC与平面SBC所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知平面α、β和直线m，给出条件：①m∥α；②m⊥α；③m?α；④α⊥β；⑤α∥β．由这五个条件中的两个同时成立能推导出m∥β的是（ ）
| A、①④ | B、①⑤ | C、②⑤ | D、③⑤ |
直线l：x+
y-4=0与圆C：x2+y2=4的位置关系是（ ）
| 3 |
| A、相交 | B、相切 |
| C、相离 | D、无法确定 |
某程序框图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=x•tanx | ||
| B、f（x）=x2+1 | ||
C、f（x）=x2+
| ||
| D、f（x）=x3•cosx |