题目内容
已知函数f(x)=
,若f(a)=1,则a的所有可能结果之和为( )
|
| A、e | ||
B、
| ||
C、e+
| ||
D、2e+
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:由分段函数可得,当0<a≤e时,令|lna|=1得a=e或a=
;当a>e,令2-lna=1,则a=e(舍去),即可得到a的所有可能之和.
| 1 |
| e |
解答:解:由于函数f(x)=
,
则当0<a≤e时,令|lna|=1得a=e或a=
;
当a>e,令2-lna=1,则a=e(舍去),
所以a的所有可能结果之和为e+
.
故选C.
|
则当0<a≤e时,令|lna|=1得a=e或a=
| 1 |
| e |
当a>e,令2-lna=1,则a=e(舍去),
所以a的所有可能结果之和为e+
| 1 |
| e |
故选C.
点评:本题考查分段函数及运用,考查分段函数值所对应的自变量的值,注意各段的自变量的范围,属于基础题.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
对非零实数x,y,z,定义运算“⊕”满足:(1)x⊕x=1;(2)x⊕(y⊕z)=(x⊕y)•z.若f(x)=e2x⊕ex-ex⊕e2x,则下列判断正确的是( )
| A、f(x)是增函数又是奇函数 | B、f(x)是减函数又是奇函数 | C、f(x)是增函数又是偶函数 | D、f(x)是减函数又是偶函数 |
若函数f(x)=ax+1在区间(-1,1)上存在一个零点,则实数a的取值范围是( )
| A、a>1 | B、a<1 | C、a<-1或a>1 | D、-1<a<1 |
定义符号函数sgnx=
,设函数f(x)=
•f1(x)+
•f2(x),x∈(0,2)其中f1(x)=x2+1,f2(x)=-2x+4.若f(f(a))∈(0,1),则实数a的取值范围是( )
|
| sgn(1-x)+1 |
| 2 |
| sgn(x-1) |
| 2 |
A、(0,
| ||||||
B、(1,
| ||||||
C、(0,
| ||||||
D、(
|
已知f(x)=
是R上的增函数,那么a的取值范围是( )
|
| A、(0,1) |
| B、(1,5) |
| C、(1,2] |
| D、[2,5) |
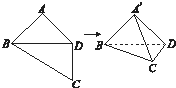 如图,四边形ABCD中,AB=AD=CD=1,BD=
如图,四边形ABCD中,AB=AD=CD=1,BD=