题目内容
17.设椭圆E:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1,一组平行直线的斜率是$\frac{3}{2}$(1)这组直线何时与椭圆相交?
(2)当它们与椭圆相交时,求它们中点的轨迹方程.
分析 (1)设这组直线为y=$\frac{3}{2}$x+m,与椭圆方程联立化为:9x2+6mx+2m2-18=0,令△>0,解得m范围即可得出.
(2)设弦AB的中点为M(x,y),A(x1,y1),B(x2,y2).则$\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{9}$=1,$\frac{{x}_{2}^{2}}{4}+\frac{{y}_{2}^{2}}{9}=1$,相减利用中点坐标公式、斜率计算公式即可得出.
解答 解:(1)设这组直线为y=$\frac{3}{2}$x+m,联立$\left\{\begin{array}{l}{y=\frac{3}{2}x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}=1}\end{array}\right.$,化为:9x2+6mx+2m2-18=0,
令△=36m2-36(2m2-18)>0,解得$-3\sqrt{2}<m<3\sqrt{2}$.
∴这组直线的截距在范围$(-3\sqrt{2},3\sqrt{2})$时与椭圆相交.
(2)设弦AB的中点为M(x,y),A(x1,y1),B(x2,y2).
则$\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{9}$=1,$\frac{{x}_{2}^{2}}{4}+\frac{{y}_{2}^{2}}{9}=1$,
相减可得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{4}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{9}$=0,
把$\frac{{x}_{1}+{x}_{2}}{2}$=x,$\frac{{y}_{1}+{y}_{2}}{2}$=y,$\frac{3}{2}$=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$,代入可得:
$\frac{2x}{4}+\frac{2y}{9}×\frac{3}{2}$=0,
化为3x+2y=0.
∴它们中点的轨迹方程是直线3x+2y=0在椭圆内部的部分.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、“中点弦”问题,考查了推理能力与计算能力,属于中档题.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | 第一象限的角 | B. | 第二象限的角 | C. | 第三象限的角 | D. | 第四象限的角 |
| A. | (-$\frac{1}{5}$,1) | B. | (-∞,-$\frac{1}{5}$)∪(1,+∞) | C. | [-$\frac{1}{5}$,1) | D. | (-∞,-$\frac{1}{5}$]∪[1,+∞) |
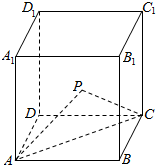 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点P为体对角线的中点.若△PAC的正视图的最高点与侧视图的每一个顶点相连所得的几何体的体积为V1,正方体外接球的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点P为体对角线的中点.若△PAC的正视图的最高点与侧视图的每一个顶点相连所得的几何体的体积为V1,正方体外接球的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为( )| A. | $\frac{1}{4π}$ | B. | $\frac{\sqrt{3}}{4π}$ | C. | $\frac{\sqrt{3}}{36π}$ | D. | $\frac{\sqrt{6}}{36π}$ |
| A. | 6 | B. | 5 | C. | 7 | D. | 4 |
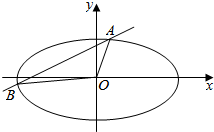 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.