题目内容
6.已知函数f(x)=log2x的定义域是[2,8].(1)设g(x)=f(2x)+f(x+2).求g(x)的解析式及定义域;
(2)求函数y=f2(x)+f(x2)的最大值和最小值.
分析 (1)根据函数的定义求解即可;
(2)利用换元法进行求解.
解答 解:(1)∵f(x)=log2x,
∴g(x)=f(2x)+f(x+2)=${log_2}^{2x}+{log_2}^{(x+2)}={log_2}^{(2{x^2}+4x)}$,(3')
因为f(x)的定义域是[2,8],所以$\left\{{\begin{array}{l}{2≤2x≤8}\\{2≤x+2≤8}\end{array}}\right.$,解之得1≤x≤4.
于是 g(x)的定义域为{x|1≤x≤4}. (6')
(2)y=(log${{\;}_{2}}^{x})^{2}$2+$lo{{g}_{2}}^{{x}^{2}}$,
=(log${{\;}_{2}}^{x})^{2}$2+2log2x,
令t=$lo{{g}_{2}}^{x}$,x∈[1,$\frac{3}{2}$],
则y=t2+2t=(t+1)2-1.
当t=1时,ymin=3;
当t=$\frac{3}{2}$时,ymax=$\frac{21}{4}$.
点评 本题主要考查函数的定义域、单调性和函数的值域的求法,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
1.已知集合A={x|0≤x≤2},B={x|x<0或x>1},则A∩B=( )
| A. | (-∞,1]∪(2,+∞) | B. | (-∞,0)∪(1,2) | C. | (1,2] | D. | (1,2) |
11.已知集合A={1,a,a-1},若-2∈A,则实数a的值为( )
| A. | -2 | B. | -1 | C. | -1或-2 | D. | -2或-3 |
15.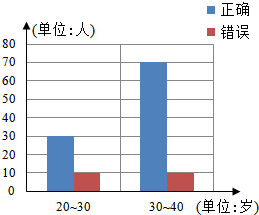 “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(理)(2)若某选手能正确回答第一、二、三、四扇门的概率分别为$\frac{4}{5}$,$\frac{3}{4}$,$\frac{2}{3}$,$\frac{1}{3}$,正确回答一个问题后,选择继续回答下一个问题的概率是$\frac{1}{2}$,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望.
每扇门对应的梦想基金:(单位:元)
(文)(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中至少有一人在20~30岁之间的概率.
 “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(理)(2)若某选手能正确回答第一、二、三、四扇门的概率分别为$\frac{4}{5}$,$\frac{3}{4}$,$\frac{2}{3}$,$\frac{1}{3}$,正确回答一个问题后,选择继续回答下一个问题的概率是$\frac{1}{2}$,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望.
| 第一扇门 | 第二扇门 | 第三扇门 | 第四扇门 |
| 1000 | 2000 | 3000 | 5000 |
(文)(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中至少有一人在20~30岁之间的概率.