题目内容
12.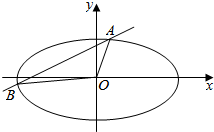 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.(I)求椭圆的方程;
(Ⅱ)直线y=$\frac{1}{2}$x+m与椭圆交于A,B两点,求△OAB面积的最大值.
分析 (I)运用椭圆的离心率公式和三角形的面积公式及a,b,c的关系,解方程可得a,b,进而得到椭圆方程;
(Ⅱ)设A(x1,y1),B(x2,y2),将y=$\frac{1}{2}$x+m代入椭圆方程,运用韦达定理和判别式大于0,由直线与y轴交于(0,m),则S△OAB=$\frac{1}{2}$|m|•|x1-x2|,化简整理,再由基本不等式即可得到最大值.
解答 解:(I)由题意可得,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$•2c•b=2$\sqrt{3}$,a2-b2=c2,
解得a=2$\sqrt{2}$,b=$\sqrt{2}$,
即有椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1;
(Ⅱ)设A(x1,y1),B(x2,y2),将y=$\frac{1}{2}$x+m代入椭圆方程x2+4y2=8,
可得x2+2mx+2m2-4=0,判别式△=4m2-4(2m2-4)>0,
解得-2<m<2且m≠0,x1+x2=-2m,x1x2=2m2-4,
由直线与y轴交于(0,m),
则S△OAB=$\frac{1}{2}$|m|•|x1-x2|=$\frac{1}{2}$|m|•$\sqrt{4{m}^{2}-4(2{m}^{2}-4)}$
=|m|•$\sqrt{4-{m}^{2}}$≤$\frac{{m}^{2}+4-{m}^{2}}{2}$=2,
当且仅当m=±$\sqrt{2}$时取得等号.
则OAB面积的最大值为2.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查三角形的面积的最值的求法,注意运用联立直线方程和椭圆方程,运用韦达定理和基本不等式,考查运算化简能力,属于中档题.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案| A. | [0,2) | B. | [0,2] | C. | (1,2) | D. | (1,2] |
| A. | (-∞,1]∪(2,+∞) | B. | (-∞,0)∪(1,2) | C. | (1,2] | D. | (1,2) |
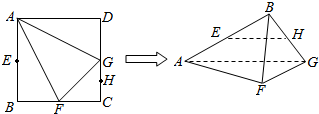
 如图1,在Rt△ABC中,∠ABC=90°,AB=BC=4,点E,F分别在线段AB,AC上,且EF∥BC,将△AEF沿EF折起到△PEF的位置,使得二面角P-EF-B的大小为60°(如图2).
如图1,在Rt△ABC中,∠ABC=90°,AB=BC=4,点E,F分别在线段AB,AC上,且EF∥BC,将△AEF沿EF折起到△PEF的位置,使得二面角P-EF-B的大小为60°(如图2).