题目内容
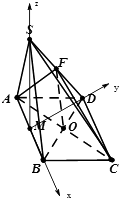
【题目】已知在四棱锥S﹣ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点. 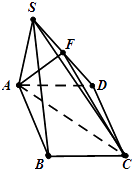
(1)证明:SB∥面ACF;
(2)求面SBC与面SAD所成锐二面角的余弦值.
【答案】
(1)证明:连接BD交AC于O,连接OF,
因为ABCD为菱形,所以OB=OD,
又F为SD的中点,所以FO∥SB,
因为FO平面ACF,SB面ACF,
所以SB∥面ACF.
(2)证明:取AB中点M,连接MD,分别以MB、MD、MS为x,y,z轴,建立空间直角坐标系.
设AB=a,则B( ![]() ,0,0),C(a,
,0,0),C(a, ![]() ,0),A(﹣
,0),A(﹣ ![]() ,0,0),D(0,
,0,0),D(0, ![]() ,0),S(0,0,
,0),S(0,0, ![]() ),
),
![]() =(
=( ![]() ,
, ![]() ,0),
,0), ![]() =(﹣
=(﹣ ![]() ),
), ![]() =(
=( ![]() ),
), ![]() =(
=( ![]() ),
),
设面SBC的法向量 ![]() ,则
,则 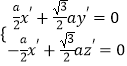 ,
,
令x′=1,则 ![]() .
.
设面SAD的法向量为 ![]() ,则
,则 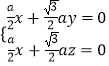 ,
,
令x=1,则 ![]() .
.
则cos< ![]() >=
>= 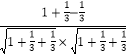 =
= ![]() ,
,
所以锐二面角的余弦值为 ![]() .
.
【解析】(1)连接BD交AC于O,连接OF,推导出FO∥SB,由此能证明SB∥面ACF.(2)取AB中点M,连接MD,分别以MB、MD、MS为x,y,z轴,建立空间直角坐系.利用向量法能求出锐二面角的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】 某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于
为大于![]() 的常数),现随机抽取
的常数),现随机抽取![]() 件合格产品,测得数据如下:
件合格产品,测得数据如下:
尺寸 |
|
|
|
|
|
|
质量 |
|
|
|
|
|
|
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的
内时为优等品,现从抽取的![]() 件合格产品中再任选
件合格产品中再任选![]() 件,记
件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.