题目内容
1.公差不为0的等差数列{an}的前n项和为Sn,S5=15,且a2,a4,a8成等比数列.(1)求{an}的通项公式;
(2)设bn=$\frac{1}{a_1^2}+\frac{1}{a_2^2}+\frac{1}{a_3^2}+…+\frac{1}{a_n^2}$,证明:bn<2.
分析 (1)设出等差数列的首项和公差,由已知得到首项和公差的两个关系式,求出首项和公差,代入等差数列的通项公式得答案.(2)利用放缩法及列项相消法得证.
解答 解:(1)在等差数列{an}中,设其首项为a1,公差为d,
∵S5=15,∴${5}_{{a}_{1}}+\frac{5×4}{2}d=15$,①
又∵a2,a4,a8成等比数列,
∴${{a}_{4}}^{2}={a}^{2}•{a}^{8}$,即${(a}_{1}+3d)^{2}=({a}_{1}+d)({a}_{1}+7d)$,②
∴由①,②得a1=1,d=1,
∴an=1+(n-1)×1=n,
∴{an}的通项公式为an=n.
(2)∵bn=1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+$\frac{1}{1×2}+$$\frac{1}{2×3}+$…$\frac{1}{(n-1)n}$
=1$+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}$$-\frac{1}{n}$
=$2-\frac{1}{n}$<2,
∴bn<2
点评 本题考查等差数列性质的综合应用及不等式的应用,解题时要注意计算能力的培养.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
6.设f(x)=|lgx|,若函数g(x)=f(x)-ax在区间(0,4)上有三个零点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{e}})$ | B. | $({\frac{lg2}{2},\frac{lge}{e}})$ | C. | $({\frac{lg2}{2},e})$ | D. | $({0,\frac{lg2}{2}})$ |
11.根据以下样本数据
得到回归方程$\widehat{y}$=bx+a,则下列说法正确的是( )
| x | 0 | 1 | 2 | 3 |
| y | 7 | 5 | 3 | 2 |
| A. | y与x正相关 | B. | 回归直线必过点(2,3) | ||
| C. | a<0,b>0 | D. | a>0,b<0 |
 如图,ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF.
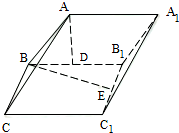
如图,ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF. 如图,已知直三棱柱ABC-A1B1C1中,AB=BC,E为AC中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=BC,E为AC中点.