题目内容
【题目】已知函数y=f(x)是定义在[0,2]上的增函数,且图像是连续不断的曲线,若f(0)=M,f(2)=N(M>0,N>0),那么下列四个命题中是真命题的有( )
A.必存在x∈[0,2],使得f(x)![]() B.必存在x∈[0,2],使得f(x)
B.必存在x∈[0,2],使得f(x)![]()
C.必存在x∈[0,2],使得f(x)![]() D.必存在x∈[0,2],使得f(x)
D.必存在x∈[0,2],使得f(x)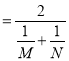
【答案】ABD
【解析】
先由题可知函数图像为![]() 上连续的增函数,再结合每个选项和不等式性质验证合理性即可
上连续的增函数,再结合每个选项和不等式性质验证合理性即可
因函数y=f(x)是定义在[0,2]上的增函数,且图像是连续不断的曲线,![]() ,所以
,所以![]() ;
;
对A,若![]() 成立,则
成立,则![]() ,即
,即![]() ,显然成立;
,显然成立;
对B,若![]() 成立,则
成立,则![]() ,即
,即![]() ,显然成立;
,显然成立;
对C,若![]() 成立,则
成立,则![]() ,先证
,先证![]() ,假设成立,则
,假设成立,则![]() ,即
,即![]() ,如
,如![]() 时,不成立,则C不成立;
时,不成立,则C不成立;
对D,若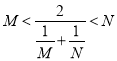 成立,则化简后为:
成立,则化简后为:![]() ,即
,即![]() ,左侧化简后
,左侧化简后![]() 成立,右侧化简后
成立,右侧化简后![]() 成立,故D成立
成立,故D成立
故选:ABD

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目