题目内容
已知射线OP分别与OA、OB都成 的角,
的角, ,则OP与平面AOB所成的角等于( )
,则OP与平面AOB所成的角等于( )
A.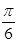 B.
B. C.
C. D.
D.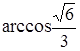
 的角,
的角, ,则OP与平面AOB所成的角等于( )
,则OP与平面AOB所成的角等于( )A.
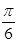 B.
B. C.
C. D.
D.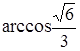
D
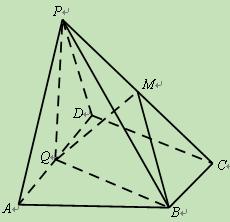
解:设点P在平面AOB中的射影为D,
∵射线OP分别与OA、OB都成 的角,
的角, ,
,
∴OD是∠AOB的平分线,∠POD是OP与平面AOB所成的角,
∴∠AOD=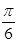 ,
,
由三余弦定理知cos∠POB=cos∠POD?cos∠AOD,
∴cos∠POD=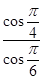 =
=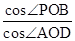 =
=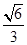
∴∠POD=arccos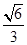 .
.
故选D.
∵射线OP分别与OA、OB都成
 的角,
的角, ,
,∴OD是∠AOB的平分线,∠POD是OP与平面AOB所成的角,
∴∠AOD=
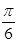 ,
,由三余弦定理知cos∠POB=cos∠POD?cos∠AOD,
∴cos∠POD=
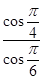 =
=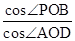 =
=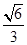
∴∠POD=arccos
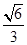 .
.故选D.

练习册系列答案
相关题目
 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆 的直径。
的直径。
 ,在圆柱
,在圆柱
 与平面
与平面 所成的角为
所成的角为
 ,当
,当 的值。
的值。
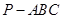 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,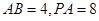 ,过
,过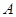 作与
作与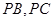 分别交于
分别交于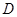 和
和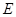 的截面,则截面
的截面,则截面
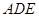 的周长的最小值是 ( )
的周长的最小值是 ( ) 为两条异面直线,
为两条异面直线, 为其公垂线,直线
为其公垂线,直线 ,则
,则 与
与
 的底面
的底面 是矩形,
是矩形, 、
、 分别是
分别是 、
、 的中点,
的中点, 底面
底面 ,
,
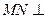 平面
平面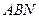
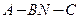 的余弦值
的余弦值
 ,点
,点 在东经1300处,点
在东经1300处,点 在西经1400处,
在西经1400处, ,则
,则 两点的球面距离为 .
两点的球面距离为 . 中,底面
中,底面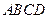 为直角梯形,
为直角梯形,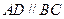 ,
,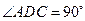 ,平面
,平面 ⊥底面
⊥底面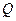 为AD的中点,
为AD的中点,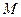 是棱
是棱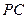 上的点,
上的点,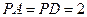 ,
,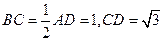 .(1)若
.(1)若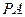
 ;(2)求证:平面
;(2)求证:平面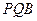 ⊥平面
⊥平面