题目内容
一直线与直二面角的两个面所成的角分别为 ,则
,则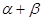 满足( )
满足( )
 ,则
,则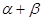 满足( )
满足( )A. | B. | C. | D. |
B
考点:
分析:设线段AB夹在直二面角α-l-β内,A∈α,B∈β,如果AB与平面α、β所成的角分别为α和β,过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点. 在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC,根据AD>AC判断∠ABC<∠ABD,由于∠ABD+∠DAB=90°进而知α+β<90°,当AB与l垂直时α+β="90°" 当AB与l平行时α+β=0,最后综合答案可得.
解答:解:设线段AB夹在直二面角α-l-β内,A∈α,B∈β,
如果AB与平面α、β所成的角分别为α和β,
过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点.
在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC
则∠DAB=α,∠ABC=β,sin∠ABC= ,sin∠DAB=
,sin∠DAB=
因为AD>AC,所以∠ABC<∠ABD,
∠ABD+∠DAB=90°,所以α+β<90°
当AB与l垂直时α+β=90°
当AB与l平行时α+β=0
∴0≤α+β≤90°
故选B
分析:设线段AB夹在直二面角α-l-β内,A∈α,B∈β,如果AB与平面α、β所成的角分别为α和β,过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点. 在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC,根据AD>AC判断∠ABC<∠ABD,由于∠ABD+∠DAB=90°进而知α+β<90°,当AB与l垂直时α+β="90°" 当AB与l平行时α+β=0,最后综合答案可得.
解答:解:设线段AB夹在直二面角α-l-β内,A∈α,B∈β,
如果AB与平面α、β所成的角分别为α和β,
过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点.
在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC
则∠DAB=α,∠ABC=β,sin∠ABC=
 ,sin∠DAB=
,sin∠DAB=
因为AD>AC,所以∠ABC<∠ABD,
∠ABD+∠DAB=90°,所以α+β<90°
当AB与l垂直时α+β=90°
当AB与l平行时α+β=0
∴0≤α+β≤90°
故选B

练习册系列答案
相关题目
 内的一条直线平行,则m//
内的一条直线平行,则m//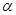
 ,则过
,则过
 ,则
,则
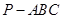 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,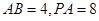 ,过
,过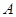 作与
作与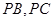 分别交于
分别交于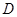 和
和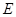 的截面,则截面
的截面,则截面
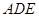 的周长的最小值是 ( )
的周长的最小值是 ( ) 为两条异面直线,
为两条异面直线, 为其公垂线,直线
为其公垂线,直线 ,则
,则 与
与 的底面
的底面 是矩形,
是矩形, 、
、 分别是
分别是 、
、 的中点,
的中点, 底面
底面 ,
,
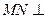 平面
平面
 的余弦值
的余弦值
 中,
中, ,又
,又 ⊥平面
⊥平面 .
. 上存在一点
上存在一点 ,使
,使 ,
, 的取值范围;
的取值范围; 的余弦值.
的余弦值.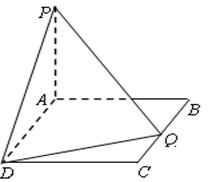
 和不同的平面
和不同的平面 ,给出下列四个说法:
,给出下列四个说法: ②
②
 ④
④