题目内容
【题目】如图(1)在等腰直角三角形![]() 中,
中,![]() ,将
,将![]() 沿中位线
沿中位线![]() 翻折得到如图(2)所示的空间图形,使二面角
翻折得到如图(2)所示的空间图形,使二面角![]() 的大小为
的大小为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() ∥
∥![]() ,
,![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,由面面垂直的判定定理即可证出平面
,由面面垂直的判定定理即可证出平面![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,所以
,所以![]() ,由(1)可知平面
,由(1)可知平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以以
,所以以![]() 为原点建立如图所示空间直角坐标系,则
为原点建立如图所示空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,利用空间向量法求解即可.
,利用空间向量法求解即可.
(1)由题意可知![]() 为
为![]() 的中位线,所以
的中位线,所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为图(2)所示的空间图形是由![]() 沿中位线
沿中位线![]() 翻折得到的,
翻折得到的,
所以![]() ,
,![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)由(1)可知二面角![]() 的平面角即为
的平面角即为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,
如图取![]() 的中点
的中点![]() ,所以
,所以![]() ,由(1)可知平面
,由(1)可知平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以以
,所以以![]() 为原点建立如图所示空间直角坐标系,
为原点建立如图所示空间直角坐标系,
设图1等腰直角![]() 中
中![]() ,则图2中
,则图2中![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以有 ,即
,即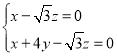 ,取
,取![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以 ,
,
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】用6个字母![]() 编拟某种信号程序(大小写有区别),把这6个字母全部排列如图所示的表格中,每个字母必须使用且只使用一次,不同的排列方式表示不同的信号,如果恰有一对字母(同一个字母的大小写)排到同一列的上下格位置,那么称此信号为“微错号”,则不同的“微错号”的总数为( )
编拟某种信号程序(大小写有区别),把这6个字母全部排列如图所示的表格中,每个字母必须使用且只使用一次,不同的排列方式表示不同的信号,如果恰有一对字母(同一个字母的大小写)排到同一列的上下格位置,那么称此信号为“微错号”,则不同的“微错号”的总数为( )
A.144B.288C.432D.576

