题目内容
(本题满分10分)某重点高校数学教育专业的三位毕业生甲、乙、丙参加了一所中学的招聘面试,面试合格者可以正式签约,毕业生甲表示只要面试合格就签约,毕业生乙和丙则约定:两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是 ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求:
(1)至少有1人面试合格的概率;(2)签约人数X的分布列.
 ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求:(1)至少有1人面试合格的概率;(2)签约人数X的分布列.
(1) ;
;
(2)分布列为:
 ;
;(2)分布列为:
| X | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
第一问中利用对立事件的概率求解,至少有1人面试合格的概率为
P=1- =
= .
.
第二问P(X=0)= ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= .
.
P(X=1)= ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= ,
,
P(X=2)= ×
× ×
× =
= .
.
P(X=3)= ×
× ×
× =
=
解:(1)至少有1人面试合格的概率为
P=1- =
= . 4分
. 4分
(2)P(X=0)= ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= .
.
P(X=1)= ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= ,
,
P(X=2)= ×
× ×
× =
= .
.
P(X=3)= ×
× ×
× =
= .
.
从而X的分布列为 10分
P=1-
 =
= .
.第二问P(X=0)=
 ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= .
.P(X=1)=
 ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= ,
,P(X=2)=
 ×
× ×
× =
= .
.P(X=3)=
 ×
× ×
× =
=
解:(1)至少有1人面试合格的概率为
P=1-
 =
= . 4分
. 4分(2)P(X=0)=
 ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= .
.P(X=1)=
 ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= ,
,P(X=2)=
 ×
× ×
× =
= .
.P(X=3)=
 ×
× ×
× =
= .
.从而X的分布列为 10分
| X | 0 | 1 | 2 | 3 |
| P |  |  |  |  |

练习册系列答案
相关题目
 成等差数列,则
成等差数列,则 .
.  ,记
,记 .
. 取得最大值和最小值时的概率; (2)求
取得最大值和最小值时的概率; (2)求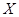 所有可能取值的集合是
所有可能取值的集合是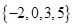 ,且
,且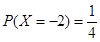 ,
,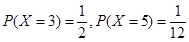 ,则
,则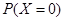 的值为:
的值为:
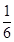

 ,求
,求 四棵风景树,受本地地理环境的影响,
四棵风景树,受本地地理环境的影响, 两棵树的成活的概率均为
两棵树的成活的概率均为 ,另外两棵树
,另外两棵树 为进口树种,其成活概率都为
为进口树种,其成活概率都为 ,设
,设 表示最终成活的树的数量.
表示最终成活的树的数量. 的值;
的值; 的取值如下表所示:
的取值如下表所示:









 ,则
,则 ______
______ ),若P(Z>2)=0.023,则P(-2≤Z≤2)=
),若P(Z>2)=0.023,则P(-2≤Z≤2)=