题目内容
随机变量ξ的分布列如图,其中a,b, 成等差数列,则
成等差数列,则 .
.
 成等差数列,则
成等差数列,则 .
. | ξ | -1 | 0 | 1 |
| P | a | b |  |
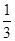
试题分析:根据题意,由于分布列中概率和为1,则可知,a+b+0.5=1,a+b=0.5,则由a,b,
 成等差数列知2b=a+
成等差数列知2b=a+
故可知
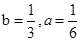 ,则可知
,则可知
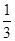 ,故可知答案为
,故可知答案为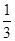 。
。点评:主要是考查了分布列的性质以及等差数列的性质的运用,属于基础题。

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
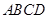 的边长为2,
的边长为2,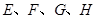 分别是边
分别是边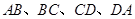 的中点.
的中点.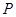 ,求满足
,求满足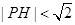 的概率;
的概率;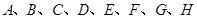 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为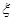 ,求随机变量
,求随机变量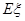 .
.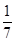 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数. 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同, 箱中没有球.我们把从
箱中没有球.我们把从 ,求
,求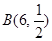 ,则P(X=3)的值是( )
,则P(X=3)的值是( )

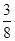

 ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求: