题目内容
5．已知各项均为正数的等比数列{an}中，3a1，$\frac{1}{2}{a_3}，2{a_2}$成等差数列，则$\frac{{{a_{11}}+{a_{13}}}}{{{a_8}+{a_{10}}}}$=27．分析 由题意可得公比q的方程，解得方程可得q，可得$\frac{{{a_{11}}+{a_{13}}}}{{{a_8}+{a_{10}}}}$=q3，代值计算可得．
解答 解：设等比数列{an}的公比为q，
由3a1，$\frac{1}{2}{a_3}，2{a_2}$成等差数列，
可得a3=3a1+2a2，
∴a1q2=3a1+2a1q，即q2=3+2q
解得q=3，或q=-1（舍去），
∴$\frac{{{a_{11}}+{a_{13}}}}{{{a_8}+{a_{10}}}}$=$\frac{（{a}_{8}+{a}_{10}）{q}^{3}}{{a}_{8}+{a}_{10}}$=q3=27，
故答案为：27．
点评 本题考查等差数列和等比数列的通项公式和性质，考查运算求解能力，属于基础题．
练习册系列答案
相关题目
16．给出下列命题：
①若给定命题p：?x∈R，使得x2+x-1＜0，则?p：?x∈R，均有x2+x-1≥0；
②若p∧q为假命题，则p，q均为假命题；
③命题“若x2-3x+2=0，则x=2”的否命题为“若 x2-3x+2=0，则x≠2，
其中正确的命题序号是（ ）
①若给定命题p：?x∈R，使得x2+x-1＜0，则?p：?x∈R，均有x2+x-1≥0；
②若p∧q为假命题，则p，q均为假命题；
③命题“若x2-3x+2=0，则x=2”的否命题为“若 x2-3x+2=0，则x≠2，
其中正确的命题序号是（ ）
| A． | ① | B． | ①② | C． | ①③ | D． | ②③ |
10．已知等比数列{an}首项为1，公比q=2，前n项和为Sn，则下列结论正确的是（ ）
| A． | ?n∈N*，Sn＜an+1 | |
| B． | ?n∈N*，an•an+1≤an+2 | |
| C． | ?n0∈N*，a${\;}_{{n}_{0}}$+a${\;}_{{n}_{0}+2}$=2a${\;}_{{n}_{0}+1}$ | |
| D． | ?n0∈N*，a${\;}_{{n}_{0}}$+a${\;}_{{n}_{0}+3}$=a${\;}_{{n}_{0}+1}$+a${\;}_{{n}_{0}+2}$ |
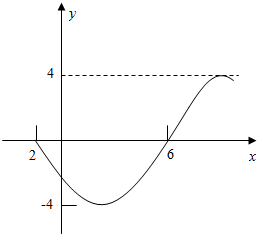函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜π，x∈R）的部分图象如图所示．