题目内容
9.函数f(x)=|sin$\frac{x}{2}$cos$\frac{x}{2}$|的最小正周期是( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
分析 由条件利用二倍角的正弦公式可得函数的解析式为f(x)=$\frac{1}{2}$|sinx|,再根据y=|Asin(ωx+φ)|的周期等于$\frac{1}{2}$•$\frac{2π}{ω}$,可得结论.
解答 解:函数f(x)=|sin$\frac{x}{2}$cos$\frac{x}{2}$|=$\frac{1}{2}$|sinx|的最小正周期是$\frac{1}{2}$•$\frac{2π}{1}$=π,
故选:C.
点评 本题主要考查三角函数的周期性及其求法,二倍角的正弦公式,利用了y=Asin(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,y=|Asin(ωx+φ)|的周期等于$\frac{1}{2}$•$\frac{2π}{ω}$,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
19.从4个不同的独唱节目和2个不同的合唱节目中选出4个节目编排一个节目单,要求最后一个节目必须是合唱,则这个节目单的编排方法共有( )
| A. | 14种 | B. | 48种 | C. | 72种 | D. | 120种 |
4.已知集合A={x|x2-2x>0},B={x|log2(x+1)<1},则A∩B等于( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (-1,0) |
18.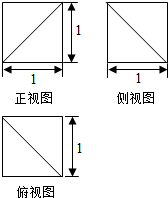 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )
 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
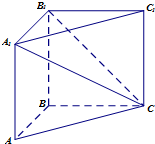 如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.
如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.