题目内容
.设函数f(x)=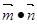 ,其中向量
,其中向量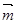 ="(2cosx,1),"
="(2cosx,1)," 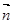 =(cosx,
=(cosx,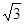 sin2x), x∈R.
sin2x), x∈R.
(1) 求f(x)的最小正周期;并求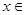
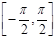 的值域和单调区间;
的值域和单调区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,f(A)=2,a=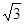 ,b+c=3(b>c),求b、c的长.
,b+c=3(b>c),求b、c的长.
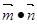 ,其中向量
,其中向量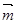 ="(2cosx,1),"
="(2cosx,1)," 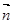 =(cosx,
=(cosx,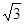 sin2x), x∈R.
sin2x), x∈R.(1) 求f(x)的最小正周期;并求
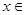
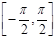 的值域和单调区间;
的值域和单调区间;(2)在△ABC中,a、b、c分别是角A、B、C的对边,f(A)=2,a=
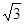 ,b+c=3(b>c),求b、c的长.
,b+c=3(b>c),求b、c的长.(1)f(x)的最小正周期为π. (2) 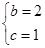 。
。
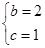 。
。本试题主要是考查了向量的数量积公式的运用和三角函数的性质的综合运用。以及解三角形的运用。
(1)因为f(x)=2cos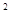 x+
x+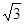 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+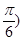 根据周期公式可知f(x)的最小正周期为π
根据周期公式可知f(x)的最小正周期为π
(2)∵f(A)=2,即1+2sin(2A+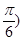 =2,
=2,
∴sin(2A+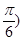 =
=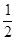
结合角A的范围得到2A+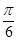 =
=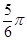 .,结合余弦定理得到角A。
.,结合余弦定理得到角A。
并得到b,c的值。
(1)f(x)=2cos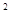 x+
x+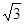 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+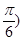
∴f(x)的最小正周期为π.
(2)∵f(A)=2,即1+2sin(2A+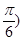 =2,
=2,
∴sin(2A+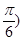 =
=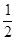
∵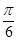 <2A+
<2A+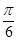 <
<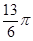 ∴2A+
∴2A+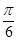 =
=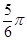 .
.
由cosA=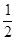 =
=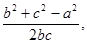 即(b+c)
即(b+c)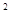 -a
-a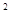 =3bc,
=3bc,
∴bc=2.又b+c=3(b>c), ∴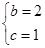
(1)因为f(x)=2cos
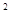 x+
x+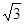 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+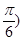 根据周期公式可知f(x)的最小正周期为π
根据周期公式可知f(x)的最小正周期为π(2)∵f(A)=2,即1+2sin(2A+
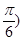 =2,
=2,∴sin(2A+
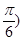 =
=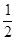
结合角A的范围得到2A+
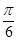 =
=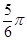 .,结合余弦定理得到角A。
.,结合余弦定理得到角A。并得到b,c的值。
(1)f(x)=2cos
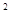 x+
x+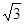 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+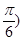
∴f(x)的最小正周期为π.
(2)∵f(A)=2,即1+2sin(2A+
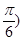 =2,
=2,∴sin(2A+
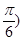 =
=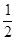
∵
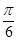 <2A+
<2A+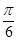 <
<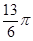 ∴2A+
∴2A+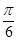 =
=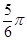 .
.由cosA=
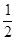 =
=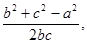 即(b+c)
即(b+c)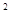 -a
-a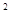 =3bc,
=3bc,∴bc=2.又b+c=3(b>c), ∴
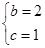

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
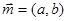 ,向量
,向量 ,向量p=(b-2,a-2)
,向量p=(b-2,a-2) ∥
∥ ,求证△ABC为等腰三角形;
,求证△ABC为等腰三角形; ,边长c=2,
,边长c=2, , 求 △ABC的面积.
, 求 △ABC的面积.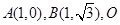 为坐标原点,点
为坐标原点,点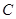 在第二象限,且
在第二象限,且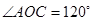 ,设
,设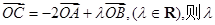 等于 ( )
等于 ( ) 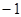
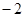
 ABC中,M是BC的中点,AM ="3,BC" =10,则
ABC中,M是BC的中点,AM ="3,BC" =10,则 =______________
=______________

 向量
向量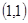 向上向左均平移1个单位后所得向量为 ;
向上向左均平移1个单位后所得向量为 ;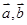 夹角为
夹角为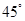 ,且
,且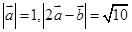 ;则
;则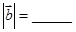
 ,
, ,
, 满足
满足 ,且
,且 ,则
,则 ,则
,则 =
=

 中,
中, 是重心,
是重心, 过
过 ,若
,若 ,则
,则 .
.