题目内容
(本小题14分)已知△ABC的角A、B、C所对的边分别为a,b,c,设向量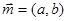 ,向量
,向量 ,向量p=(b-2,a-2)
,向量p=(b-2,a-2)
(1)若 ∥
∥ ,求证△ABC为等腰三角形;
,求证△ABC为等腰三角形;
(2)若 ⊥
⊥ ,边长c=2,
,边长c=2, , 求 △ABC的面积.
, 求 △ABC的面积.
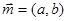 ,向量
,向量 ,向量p=(b-2,a-2)
,向量p=(b-2,a-2)(1)若
 ∥
∥ ,求证△ABC为等腰三角形;
,求证△ABC为等腰三角形;(2)若
 ⊥
⊥ ,边长c=2,
,边长c=2, , 求 △ABC的面积.
, 求 △ABC的面积.(1)见解析。(2)
试题分析:(1)证明:∵m∥n,∴asinA=bsinB.
由正弦定理得a2=b2,a=b,∴△ABC为等腰三角形 ……………………6分
(2)∵m⊥p,∴m·p=0.即a(b-2)+b(a-2)=0
∴a+b=ab. ……………………8分
由余弦定理得4=a2+b2-ab=(a+b)2-3ab
即(ab)2-3ab-4=0,∴ab=4或ab=-1(舍)
∴S△ABC=absinC=×4×sin=……………………14分
点评:三角函数和向量相结合往往是第一道大题,一般较为简单,应该是必得分的题目。而有些同学在学习中认为这类题简单,自己一定会,从而忽略了对它的练习,因此导致考试时不能得满分,甚至不能得分。因此我们在平常训练的时候就要要求自己“会而对,对而全”。

练习册系列答案
相关题目
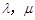 ,使得
,使得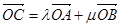 ,则
,则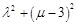 的取值范围是 .
的取值范围是 . 中
中 ,点
,点 的斜坐标定义为:“若
的斜坐标定义为:“若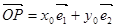 (其中
(其中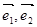 分别为与斜坐标系的
分别为与斜坐标系的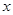 轴,
轴,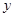 轴同方向的单位向量),则点
轴同方向的单位向量),则点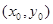 ”.若
”.若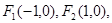 且动点
且动点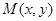 满足
满足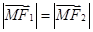 ,则点
,则点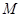 在斜坐标系中的轨迹方程为( )
在斜坐标系中的轨迹方程为( )



 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则
 ,
, ,且
,且 与
与 互相垂直,则
互相垂直,则 的值是
的值是 .
.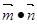 ,其中向量
,其中向量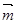 ="(2cosx,1),"
="(2cosx,1)," 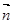 =(cosx,
=(cosx,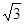 sin2x), x∈R.
sin2x), x∈R.
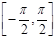 的值域和单调区间;
的值域和单调区间;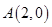 ,
,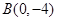 ,
, 为坐标原点,点
为坐标原点,点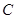 在第四象限内,且
在第四象限内,且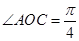 ,设
,设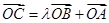
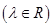 ,则
,则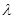 的值是( )
的值是( )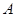 .
.
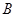 .
.

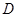 .
.
 (λ为常数),这里点P、Q的坐标分别为
(λ为常数),这里点P、Q的坐标分别为 中,
中, 边的高为
边的高为 ,若
,若 ,
, ,
, ,
, ,
, ,则
,则



