题目内容
【题目】如图所示，正方体ABCD－A1B1C1D1中，M、N分别是A1B1、B1C1的中点，问：
(1)AM和CN是否是异面直线？说明理由；
(2)D1B和CC1是否是异面直线？说明理由．
【答案】（1）不是异面直线（2）是异面直线
【解析】试题分析：（1）根据公理4得MN∥A1C1∥AC，所以两直线共面（2）由异面直线判定定理可得两直线为异面直线
试题解析：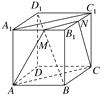
(1)不是异面直线，理由：连结MN，A1C1、AC，如图，因为M、N分别是A1B1、B1C1的中点，所以MN∥A1C1.又因为A1A
D1D，D1D
C1C，所以A1A
C1C，四边形A1ACC1为平行四边形，所以A1C1∥AC，故MN∥A1C1∥AC，所以A、M、N、C在同一个平面内，故AM和CN不是异面直线．
(2)是异面直线，证明如下：假设D1B与CC1在同一个平面CC1D1内，则B∈平面CC1D1，C∈平面CC1D1，所以BC平面CC1D1，这显然是不正确的，所以假设不成立，故D1B与CC1是异面直线．
练习册系列答案
相关题目
【题目】某公司有
五辆汽车，其中
两辆汽车的车牌尾号均为1. 
两辆汽车的车牌尾号均为2， 
车的车牌尾号为6，已知在非限行日，每辆车可能出车或不出车， 
三辆汽车每天出车的概率均为
， 
两辆汽车每天出车的概率均为
，且五辆汽车是否出车相互独立，该公司所在地区汽车限行规定如下：
车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
（1）求该公司在星期一至少有2辆汽车出国的概率；
（2）设
表示该公司在星期二和星期三两天出车的车辆数之和，求
的分布列及期望.
