题目内容
13.已知函数f(x)=ex,h(x)=k(x+1)(1)当函数f(x)的图象恒在h(x)的图象上方时,求正实数k的取值范围.
(2)当函数f(x)-h(x)有两个零点x1,x2时,证明:x1+x2>0.
分析 (1)作出函数的图象,利用导数的几何意义求出切线斜率,利用数形结合即可得到结论;
(2)先求出x2-x1=ln$\frac{{x}_{2}+1}{{x}_{1}+1}$,令t=$\frac{{x}_{2}+1}{{x}_{1}+1}$,求出x1+x2=$\frac{lnt}{t-1}$+$\frac{tlnt}{t-1}$-2,问题转化为证明lnt>$\frac{2(t-1)}{t+1}$,构造函数F(t)=lnt-$\frac{2(t-1)}{t+1}$,通过函数的单调性证明即可.
解答 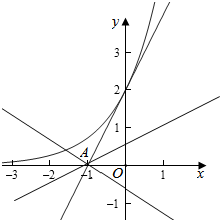 解:(1)若函数f(x)图象恒在函数h(x)图象的上方(没有交点),
解:(1)若函数f(x)图象恒在函数h(x)图象的上方(没有交点),
即f(x)-h(x)>0恒成立,
即ex-k(x+1)>0,
即ex>k(x+1),
当k>0时,g(x)=k(x+1)过定点(-1,0),
函数f(x)的导数为f′(x)=ex,
设切点为(a,b),则对应的切线斜率k=f′(a)=ea,
则对应的切线方程为y-ea=ea(x-a),
∵直线过点(-1,0),
∴-ea=ea(-1-a),
解得a=0,此时切线斜率k=f′(0)=1,
即此时k=1,
则解得0<k<1;
(2)设x2>x1,
由题意得:$\left\{\begin{array}{l}{{e}^{{x}_{1}}=k{(x}_{1}+1)}\\{{e}^{{x}_{2}}=k{(x}_{2}+1)}\end{array}\right.$,
∴x1=lnk+ln(x1+1)①,
x2=lnk+lnx2+1)②,
②-①得:x2-x1=ln$\frac{{x}_{2}+1}{{x}_{1}+1}$③,
令t=$\frac{{x}_{2}+1}{{x}_{1}+1}$,则t>1,x2=t(x1+1)-1,
∴③可化为:t(x1+1)-1-x1=lnt,
∴x1+1=$\frac{lnt}{t-1}$,x2+1=$\frac{tlnt}{t-1}$,
∴x1+x2=$\frac{lnt}{t-1}$+$\frac{tlnt}{t-1}$-2,
要证:x1+x2>0,
只需证:$\frac{lnt}{t-1}$+$\frac{tlnt}{t-1}$>2,
即证:lnt>$\frac{2(t-1)}{t+1}$,
构造函数F(t)=lnt-$\frac{2(t-1)}{t+1}$,
则F′(t)=$\frac{1}{t}$-$\frac{2(t+1)-2(t-1)}{{(t+1)}^{2}}$=$\frac{{(t-1)}^{2}}{{t(t+1)}^{2}}$≥0,
∴F(t)在(1,+∞)递增,
∴F(t)>F(1)=0,
∴x1+x2>0.
点评 本题考查了函数的单调性问题,考查导数的应用,转化思想,(2)中求出x1+x2,问题转化为构造新函数通过求导得到单调性是解题的关键,本题有一定的难度.

| A. | 模型1 | B. | 模型2 | C. | 模型3 | D. | 模型4 |
| A. | aabb>(ab)${\;}^{\frac{a+b}{2}}$ | B. | aabb<(ab)${\;}^{\frac{a+b}{2}}$ | ||
| C. | aabb=(ab)${\;}^{\frac{a+b}{2}}$ | D. | aabb与(ab)${\;}^{\frac{a+b}{2}}$的大小不能确定 |