题目内容
【题目】已知四棱锥P﹣ABCD的底面为矩形,PA⊥平面ABCD,PA=AB=2,AD=1,点M为PC中点,过A、M的平面α与此四棱锥的面相交,交线围成一个四边形,且平面α⊥平面PBC. 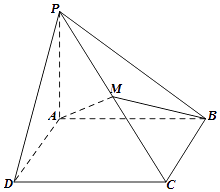
(1)在图中画出这个四边形(不必说出画法和理由);
(2)求平面α与平面ABM所成锐二面角的余弦值.
【答案】
(1)解:取PB中点N,连接AN,DM,MN,
则MN∥AD,MN与AD确定平面α
(2)解:分别以AD、AB、AP所在直线为x、y、z轴建立如图直角坐标系,
∵PA=AB=2,AD=1,点M为PC中点,N为PB中点,
∴ ![]() ,
,
![]() ,
, ![]() ,
,
设平面AMB的法向量 ![]() ,
,
则由 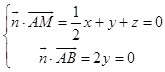 ,取x=2,得
,取x=2,得 ![]() .
.
平面α的法向量 ![]() ,
,
∴平面α与平面AMB所成二面角的余弦值 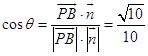 .
.
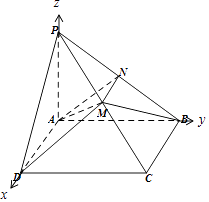
【解析】(1)取PB中点N,连接AN,DM,MN,则MN∥AD,由公理2的推论可得平面α;(2)分别以AD、AB、AP所在直线为x、y、z轴建立如图直角坐标系,由已知求得所用点的坐标,进一步求得平面α与平面ABM的法向量,由法向量所成角的余弦值可得平面α与平面ABM所成锐二面角的余弦值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目