题目内容
已知函数f(x)=x(ln x-ax)有两个极值点,则实数a的取值范围是( ).
| A.(-∞,0) | B.(0,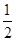 ) ) | C.(0,1) | D.(0,+∞) |
B
f′(x)=(ln x-ax)+x(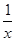 -a)=ln x+1-2ax,
-a)=ln x+1-2ax,
令f′(x)=0,得2a=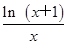 ,
,
设φ(x)=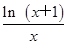 ,则φ′(x)=
,则φ′(x)=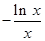 ,
,
易知φ(x)在(0,1)上递增,在(1,+∞)上递减,
∴φ(x)在(0,+∞)上的极大值为φ(1)=1.
大致图象如图
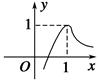
若f(x)有两个极值点,y=2a和y=φ(x)图象有两个交点,∴0<2a<1,∴0<a<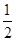 .
.
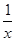 -a)=ln x+1-2ax,
-a)=ln x+1-2ax,令f′(x)=0,得2a=
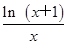 ,
,设φ(x)=
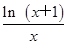 ,则φ′(x)=
,则φ′(x)=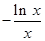 ,
,易知φ(x)在(0,1)上递增,在(1,+∞)上递减,
∴φ(x)在(0,+∞)上的极大值为φ(1)=1.
大致图象如图

若f(x)有两个极值点,y=2a和y=φ(x)图象有两个交点,∴0<2a<1,∴0<a<
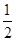 .
.
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
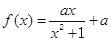 ,
,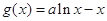 (
(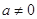 ).
).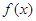 的单调区间;
的单调区间;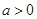 时,对于任意
时,对于任意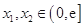 ,总有
,总有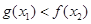 成立.
成立.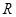 上的函数
上的函数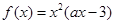 ,其中
,其中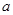 为常数.
为常数.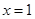 是函数
是函数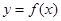 的一个极值点,求
的一个极值点,求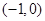 上是增函数,求实数
上是增函数,求实数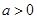 时,若
时,若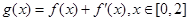 ,在
,在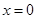 处取得最大值,求实数
处取得最大值,求实数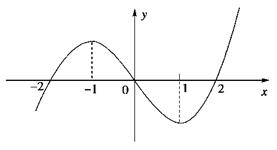
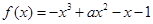 在
在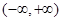 上是单调减函数,则实数
上是单调减函数,则实数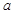 的取值范围是___________.
的取值范围是___________.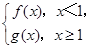 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.