题目内容
可导函数 的导函数为
的导函数为 ,且满足:①
,且满足:①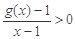 ;②
;② ,记
,记 ,
,  ,
, 则
则 的大小顺序为( )
的大小顺序为( )
 的导函数为
的导函数为 ,且满足:①
,且满足:①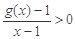 ;②
;② ,记
,记 ,
,  ,
, 则
则 的大小顺序为( )
的大小顺序为( )A. | B. | C. | D. |
C
试题分析:因为
 是减函数,则根据复合函数可知
是减函数,则根据复合函数可知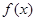 是增函数,构造函数
是增函数,构造函数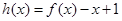 ,则
,则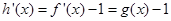 ,因为
,因为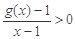 ,所以当
,所以当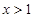 时
时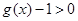 ,所以
,所以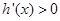 ,所以
,所以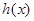 在
在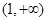 上单调递增,所以
上单调递增,所以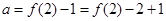 ,
,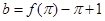 ,
,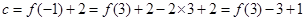 ,而
,而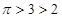 ,所以
,所以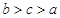 ,故选C.
,故选C.
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
题目内容
 的导函数为
的导函数为 ,且满足:①
,且满足:①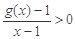 ;②
;② ,记
,记 ,
,  ,
, 则
则 的大小顺序为( )
的大小顺序为( )A. | B. | C. | D. |
 是减函数,则根据复合函数可知
是减函数,则根据复合函数可知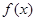 是增函数,构造函数
是增函数,构造函数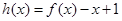 ,则
,则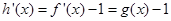 ,因为
,因为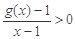 ,所以当
,所以当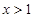 时
时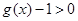 ,所以
,所以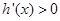 ,所以
,所以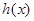 在
在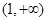 上单调递增,所以
上单调递增,所以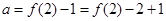 ,
,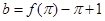 ,
,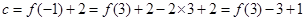 ,而
,而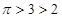 ,所以
,所以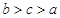 ,故选C.
,故选C.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案