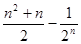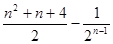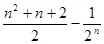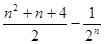题目内容
已知数列{an}满足:a1=20,a2=7,an+2﹣an=﹣2(n∈N*).
(Ⅰ)求a3,a4,并求数列{an}通项公式;
(Ⅱ)记数列{an}前2n项和为S2n,当S2n取最大值时,求n的值.
(Ⅰ)求a3,a4,并求数列{an}通项公式;
(Ⅱ)记数列{an}前2n项和为S2n,当S2n取最大值时,求n的值.
(1) ,
, ;(2)
;(2)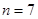 .
.
 ,
, ;(2)
;(2)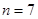 .
.试题分析:本题考查等差数列的通项公式和前
 项和公式等基础知识,考查化归与转化的思想方法,考查运算能力,考查分析问题和解决问题的能力.第一问,分
项和公式等基础知识,考查化归与转化的思想方法,考查运算能力,考查分析问题和解决问题的能力.第一问,分 是奇数,
是奇数, 是偶数两种情况,按等差数列的通项公式分别求解;第二问,分组求和,分2组按等差数列的前
是偶数两种情况,按等差数列的通项公式分别求解;第二问,分组求和,分2组按等差数列的前 项和公式求和,再按二次函数的性质求最大值.
项和公式求和,再按二次函数的性质求最大值.试题解析:(I)∵
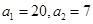 ,
, ,
,∴
 ,
,由题意可得数列
 奇数项、偶数项分布是以﹣2为公差的等差数列
奇数项、偶数项分布是以﹣2为公差的等差数列当
 为奇数时,
为奇数时,
当
 为偶数时,
为偶数时,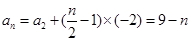
∴

(II)



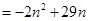
结合二次函数的性质可知,当
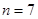 时最大.
时最大.
练习册系列答案
相关题目
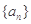 的前
的前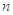 项和为
项和为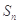 ,且
,且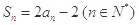 ,数列
,数列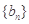 满足
满足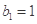 ,且点
,且点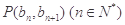 在直线
在直线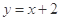 上.
上.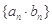 的前
的前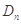 .
.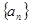 是等差数列,
是等差数列,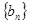 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且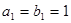 ,
,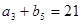 ,
,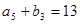 .
.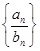 的前
的前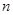 项和
项和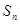 .
.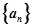 的前n项和为
的前n项和为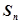 ,且
,且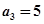 ,
,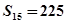 .
. 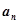 ;(2)设
;(2)设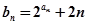 ,求数列
,求数列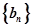 的前n项和
的前n项和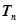 .
. 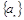 的前
的前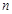 项和为
项和为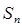 .且
.且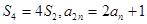
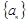 的通项公式;
的通项公式;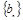 满足:
满足: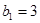 ,
,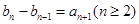 ,求数列
,求数列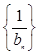 的前
的前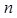 项和
项和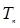 .
. 满足:三数
满足:三数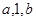 的倒数成等差数列,则
的倒数成等差数列,则 的最小值为( )
的最小值为( )
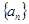 的首项为
的首项为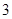 ,
,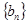 为等差数列且
为等差数列且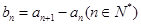 .若则
.若则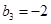 ,
,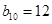 ,则
,则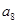 =( )
=( )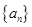 满足
满足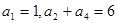 ,且对任意
,且对任意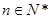 ,函数
,函数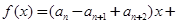
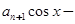
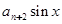 满足
满足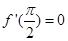 ,若
,若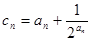 ,则数列
,则数列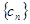 的前
的前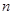 项和
项和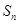 为( )
为( )