题目内容
设等差数列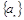 的前
的前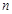 项和为
项和为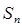 .且
.且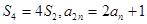
(1)求数列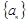 的通项公式;
的通项公式;
(2)数列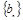 满足:
满足: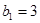 ,
,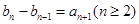 ,求数列
,求数列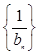 的前
的前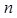 项和
项和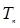 .
.
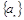 的前
的前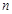 项和为
项和为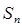 .且
.且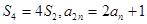
(1)求数列
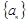 的通项公式;
的通项公式;(2)数列
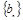 满足:
满足: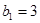 ,
,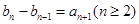 ,求数列
,求数列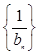 的前
的前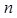 项和
项和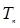 .
.(1)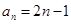 ;(2)
;(2) .
.
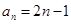 ;(2)
;(2) .
.试题分析:(1)根据等差数列的通项公式、求和公式把已知等式
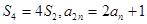 表示成首项
表示成首项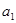 与公差
与公差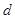 的等式, 解方程组求得首项与公差,从而得出数列
的等式, 解方程组求得首项与公差,从而得出数列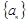 的通项公式;(2)有累加原理把
的通项公式;(2)有累加原理把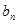 表示为
表示为 ,利用
,利用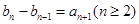 则可转化为
则可转化为 ,
, ,可用裂项相消法求出数列数列
,可用裂项相消法求出数列数列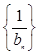 的前
的前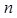 项和
项和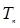
试题解析:(1)
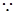
 ,
,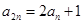 ,
,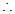
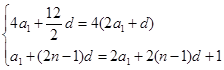 ,解得
,解得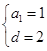 ,
,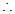
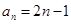 . 6分
. 6分 (2)由
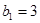 ,当
,当 时,
时,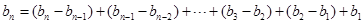
 (
(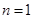 也成立).
也成立).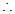
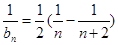 , 9分
, 9分 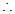
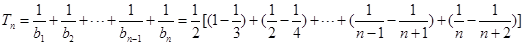
 . 13分
. 13分 
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 满足:
满足: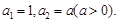 数列
数列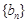 满足
满足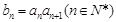 。
。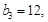 求
求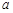 的值及
的值及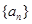 ,公差
,公差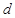 不为零,
不为零,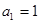 ,且
,且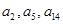 成等比数列;
成等比数列;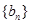 满足
满足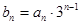 ,求数列
,求数列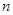 项和
项和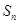 .
.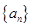 ,
,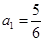 ,若以
,若以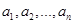 为系数的二次方程:
为系数的二次方程: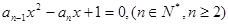 都有根
都有根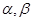 满足
满足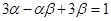 .
.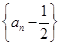 为等比数列
为等比数列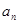 .
.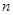 项和
项和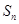 .
.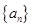 是以2为首项,1为公差的等差数列,
是以2为首项,1为公差的等差数列,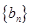 是以1为首项,2为公比的等比数列,则
是以1为首项,2为公比的等比数列,则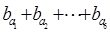 等于( )
等于( )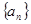 的前
的前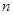 项和为
项和为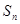 ,若
,若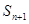 ,
,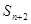 成等差数列,则其公比
成等差数列,则其公比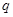 为 ( )
为 ( )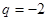
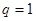
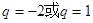
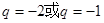
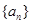 的前
的前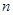 项和是
项和是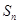 ,若数列
,若数列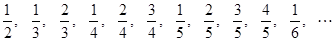 ,
,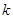 ,使
,使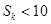 ,
,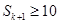 ,则
,则 .
. 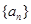 的前
的前 项和为
项和为 ,那么
,那么 的最大值为( )
的最大值为( )