题目内容
8.已知二次函数f(x)=ax2+bx满足f(0)=f(1),且f(x)的最小值为-$\frac{1}{4}$.(1)求函数f(x)的解析式;
(2)若不等式f(x)≥tx-1对x∈[$\frac{1}{2}$,3]恒成立,求实数t的取值范围;
(3)设g(x)=$\frac{f(x)+1}{x}$,若方程g(x)=t-1在x∈[$\frac{1}{2}$,3]有实根,求实数t的取值范围.
分析 (1)根据二次函数f(x)=ax2+bx满足f(0)=f(1),且f(x)的最小值为-$\frac{1}{4}$,构造方程组,求出a,b的值,可得函数f(x)的解析式;
(2)若不等式f(x)≥tx-1对x∈[$\frac{1}{2}$,3]恒成立,则x+$\frac{1}{x}$-1≥t对x∈[$\frac{1}{2}$,3]恒成立,结合对勾函数的图象和性质,可得实数t的取值范围;
(3)g(x)=$\frac{f(x)+1}{x}$=x+$\frac{1}{x}$-1,结合对勾函数的图象和性质,可得g(x)的值域为[1,$\frac{7}{3}$],进而得到答案.
解答 解:(1)∵二次函数f(x)=ax2+bx满足f(0)=f(1),且f(x)的最小值为-$\frac{1}{4}$.
∴$\left\{\begin{array}{l}a>0\\-\frac{b}{2a}=\frac{1}{2}\\ \frac{-{b}^{2}}{4a}=-\frac{1}{4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=1\\ b=-1\end{array}\right.$,
∴f(x)=x2-x;
(2)若不等式f(x)≥tx-1对x∈[$\frac{1}{2}$,3]恒成立,
即x2-x≥tx-1对x∈[$\frac{1}{2}$,3]恒成立,
即x+$\frac{1}{x}$-1≥t对x∈[$\frac{1}{2}$,3]恒成立,
∵当x=1时,x+$\frac{1}{x}$-1取最小值1,故t≤1;
(3)g(x)=$\frac{f(x)+1}{x}$=x+$\frac{1}{x}$-1,
当x=1时,g(x)取最小值1,当x=3时,g(x)取最大值$\frac{7}{3}$,
若方程g(x)=t-1在x∈[$\frac{1}{2}$,3]有实根,
则t-1∈[1,$\frac{7}{3}$],
故t∈[2,$\frac{10}{3}$].
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

| A. | {1,2} | B. | {0,1,2} | C. | ($\frac{1}{2}$,2] | D. | {1,2,3} |
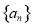 ,
,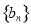 都是等差数列,若
都是等差数列,若 ,则
,则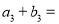 _____________.
_____________.