题目内容
14.一个所有棱长均为$\sqrt{2}$的正三棱锥(底面是正三角形,顶点在底面的射影是底面的中心)的顶点与底面的三个顶点均在某个球的球面上,则此球的体积为$\frac{\sqrt{3}}{2}$.分析 求出正四棱锥底面对角线的长,判断底面对角线长,就是球的直径,即可求出球的体积.
解答 解:正三棱锥的边长为$\sqrt{2}$,则该正三棱锥所在的正方体也为外接球的内接几何体.
所以正方体的体对角线为外接球的直径.
正方体的边长为1,所以所求球的半径为:r=$\frac{\sqrt{3}}{2}$,
所以球的体积为:V球=$\frac{4}{3}π(\frac{\sqrt{3}}{2})^{3}=\frac{\sqrt{3}}{2}π$.
故答案为:$\frac{\sqrt{3}}{2}$
点评 本题是中档题,考查空间想象能力,注意正三棱锥和正方体的转化,正方体额对角线的长是球的直径是解题的关键点,考查计算能力.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
6.在平面直角坐标系中,O为坐标原点,A(1,0),B(0,-$\sqrt{3}$),点D是圆C:(x+1)2+y2=1上的动点,则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|的最大值为( )
| A. | 2 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$+$\sqrt{2}$ | D. | $\sqrt{3}$+2 |
3.已知点P(x,y)的坐标满足|x|+|y|≤1,那么2x+y的最小值是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
4.在△ABC中,A=60°,若a,b,c成等比数列,则$\frac{bsinB}{c}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
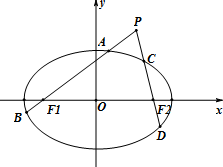 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.