题目内容
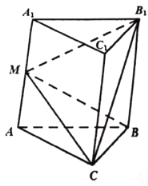
【题目】在三棱柱![]() 中,底面
中,底面![]() 是等腰三角形,且
是等腰三角形,且![]() ,侧面
,侧面![]() 是菱形,
是菱形,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1) 证明见解析;(2) ![]()
【解析】
(1)证明直线![]() 垂直
垂直![]() 所在的平面
所在的平面![]() ,从而证明
,从而证明![]() ;
;
(2)以A为原点,![]() 为x轴正方向,
为x轴正方向,![]() 为y轴正方向,垂直平面ABC向上为z轴正方向建立平面直角坐标系,设
为y轴正方向,垂直平面ABC向上为z轴正方向建立平面直角坐标系,设![]() ,线面角为
,线面角为![]() ,可得面
,可得面![]() 的一个法向量
的一个法向量![]() ,
,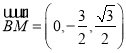 ,代入公式
,代入公式![]() 进行求值.
进行求值.

(1)证明:在![]() 中,
中,![]() 是直角,即
是直角,即![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() .
.
在菱形![]() 中,
中,![]() ,连接
,连接![]() ,
,![]()
则![]() 是正三角形,
是正三角形,
∵点![]() 是
是![]() 中点,
中点,![]() .
.
又![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]()
![]() .
.
(2)作![]() 于G,连结
于G,连结![]() .
.
由(1)知![]() 平面
平面![]() ,得到
,得到![]() ,
,
又![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]()
![]() ,
,
又平面![]() 平面
平面![]() ,
,
作![]() 于点H,则
于点H,则![]() 平面
平面![]() ,则
,则![]() 即为所求线面角.
即为所求线面角.
设![]() ,
,
由已知得![]() ,
,
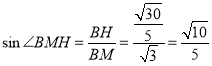 ,
,
则BM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
【题目】某城市自2014年至2019年每年年初统计得到的人口数量如表所示.
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:万) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)设第![]() 年的人口数量为
年的人口数量为![]() (2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2)研究统计人员用函数![]() 拟合该城市的人口数量,其中
拟合该城市的人口数量,其中![]() 的单位是年.假设2014年初对应
的单位是年.假设2014年初对应![]() ,
,![]() 的单位是万.设
的单位是万.设![]() 的反函数为
的反函数为![]() ,求
,求![]() 的值(精确到0.1),并解释其实际意义.
的值(精确到0.1),并解释其实际意义.