题目内容
【题目】已知动点![]() 到直线
到直线![]() 的距离比到定点
的距离比到定点![]() 的距离大1.
的距离大1.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
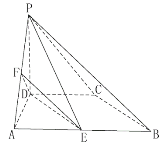
(2)若![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
①求证:![]() 轴;
轴;
②直线![]() 是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
【答案】(1)![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() .
.
【解析】
(1)由题意知,动点![]() 到直线
到直线![]() 的距离等于到定点
的距离等于到定点![]() 的距离,符合抛物线的定义,求轨迹
的距离,符合抛物线的定义,求轨迹![]() 的方程为
的方程为![]() ;
;
(2)①设动点![]() ,
,![]() ,
,![]() ,利用导数求出切线
,利用导数求出切线![]() 的方程分别为:
的方程分别为:![]() 、
、![]() ,从而有
,从而有![]() ,
,![]() 为方程
为方程![]() 的两根,证明点
的两根,证明点![]() 的横坐标与点
的横坐标与点![]() 的横坐标相等,从而证得
的横坐标相等,从而证得![]() 轴;
轴;
②由①中的结论,把直线![]() 的方程写成含有参数
的方程写成含有参数![]() 的形式,即
的形式,即![]()
并把方程看成关于![]() 的一次函数,从而得到定点为
的一次函数,从而得到定点为![]() 。
。
(1)由动点![]() 到直线
到直线![]() 的距离比到定点
的距离比到定点![]() 的距离大1得,
的距离大1得,
动点![]() 到直线
到直线![]() 的距离等于到定点
的距离等于到定点![]() 的距离,
的距离,
所以点![]() 的轨迹为顶点在原点、开口向上的抛物线,其中
的轨迹为顶点在原点、开口向上的抛物线,其中![]() ,
,
轨迹方程为![]() .
.
(2)①设切点![]() ,
,![]() ,
,![]() ,所以切线
,所以切线![]() 的斜率为
的斜率为![]() ,
,
切线![]() .
.
设![]() ,则有
,则有![]() ,化简得
,化简得![]() .
.
同理可得![]() .
.
所以![]() ,
,![]() 为方程
为方程![]() 的两根.
的两根.
则有![]() ,
,![]() ,所以
,所以![]() .
.
因此![]() 轴.
轴.
② 因为![]()
![]() ,
,
所以![]() .又因为
.又因为![]() ,
,
所以直线![]() ,即
,即![]() .
.
即直线过定点![]() .
.

练习册系列答案
相关题目