题目内容
已知曲线 的参数方程为
的参数方程为
 是参数
是参数 ,
, 是曲线
是曲线 与
与 轴正半轴的交点.以坐标原点
轴正半轴的交点.以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 与曲线
与曲线 只有一个公共点的直线
只有一个公共点的直线 的极坐标方程.
的极坐标方程.
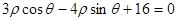
解析试题分析:首先利用平方和为1的技巧得到圆的普通方程,然后根据相切的性质求得直线的方程,最后利用极坐标公式得到直线的极坐标方程.
试题解析:把曲线 的参数方程
的参数方程
 是参数
是参数 化为普通方程得
化为普通方程得 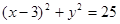 .
.
∴曲线 是圆心为
是圆心为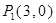 ,半径等于
,半径等于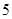 的圆.
的圆.
∵ 是曲线
是曲线 与
与 轴正半轴的交点,
轴正半轴的交点,
∴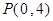 .
.
根据已知得直线 是圆
是圆 经过点
经过点 的切线.
的切线.
∵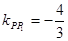 ,
,
∴直线 的斜率
的斜率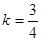 .
.
∴直线 的方程为
的方程为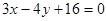 .
.
∴直线 的极坐标方程为
的极坐标方程为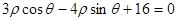 .
.
考点:圆的参数方程和普通方程,直线的直角坐标方程和极坐标方程的互化.

练习册系列答案
相关题目
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是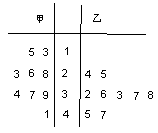
| A.62 | B.63 | C.64 | D.65 |
 :
: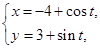 (t为参数), C
(t为参数), C :
: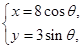 (
(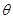 为参数)。
为参数)。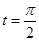 ,Q为C
,Q为C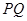 中点
中点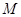 到直线
到直线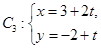 (t为参数)距离的最小值。
(t为参数)距离的最小值。 的极坐标方程是
的极坐标方程是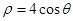 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 是参数).若直线
是参数).若直线 的值.
的值. 中,曲线
中,曲线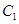 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线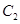 的极坐标方程为
的极坐标方程为 (
( )
)  :
:  (
( 为参数)过曲线
为参数)过曲线 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线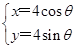 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为 .
. 有相同的长度单位,以原点
有相同的长度单位,以原点 为极点,以
为极点,以 轴正半轴为极轴.已知直线
轴正半轴为极轴.已知直线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
. 两点,求弦长
两点,求弦长 .
.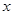 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 的值及直线的直角坐标方程;
的值及直线的直角坐标方程; ,(
,( 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系.  .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
( 是参数).
是参数). 参数方程转化为普通方程;
参数方程转化为普通方程; ,试求实数
,试求实数 值.
值.