题目内容
17.计算:$\underset{lim}{n→∞}$$\frac{n(n-1)}{2+4+6+…+2n}$=1.分析 由等差数列可知$\frac{n(n-1)}{2+4+6+…+2n}$=$\frac{n(n-1)}{\frac{(2+2n)n}{2}}$,从而解得.
解答 解:$\underset{lim}{n→∞}$$\frac{n(n-1)}{2+4+6+…+2n}$
=$\underset{lim}{n→∞}$$\frac{n(n-1)}{\frac{(2+2n)n}{2}}$
=$\underset{lim}{n→∞}$$\frac{n-1}{n+1}$=1.
故答案为:1.
点评 本题考查了等差数列的应用及极限的求法及应用.

练习册系列答案
相关题目
8.若将二次函数的图象向下、向右各平移2个单位长度得到图象的解析式为y=-x2,则原二次函数的解析式为( )
| A. | y=-(x-2)2+2 | B. | y=-(x+2)2+2 | C. | y=-(x+2)2-2 | D. | y=-(x-2)2-2 |
9.生产一定数量的商品的全部费用称为市生产成本,某企业一个月生产某种商品x万件时的生产成本为C(x)=$\frac{1}{2}$x2+2x+20(万元),每一万件售价是20万元,且生产的产品全部售完,则该企业一个月的利润Q(x)=( )
| A. | $\frac{1}{2}$x2-18x+20 | B. | -$\frac{1}{2}$x2+18x-20 | C. | $\frac{1}{2}$x2+2x | D. | $\frac{1}{2}$x2-18x |
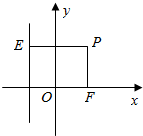 如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).
如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).