题目内容
6.已知函数f(x)是定义域为R上的偶函数,且在区间[0,+∞)上是单调递增函数,若实数a满足不等式f(log2a)+f(${log_{\frac{1}{2}}}a$)≤2f(2),则实数a的取值范围是$[{\frac{1}{4},4}]$.分析 根据函数奇偶性和单调性之间的关系,将不等式进行转化即可.
解答 解:∵f(x)是定义域为R上的偶函数,
∴不等式$f({{{log}_2}a})+f({{{log}_{\frac{1}{2}}}a})≤2f(2)$,等价为2f(log2a)≤2f(2),
即f(log2a)≤f(2),
则f(|log2a|)≤f(2),
∵在区间[0,+∞)上是单调递增函数,
∴|log2a|≤2,
即-2≤log2a≤2,
解得$\frac{1}{4}$≤a≤4,
故答案为:$[{\frac{1}{4},4}]$
点评 本题主要考查不等式的求解,结合函数奇偶性和单调性之间的关系以及对数的运算性质是解决本题的关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.一个几何体的三视图如图所示,则这个几何体的体积为( )
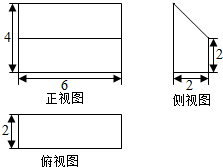

| A. | 9 | B. | 10 | C. | 36 | D. | 72 |
15.某电子广告牌连续播出四个广告,假设每个广告所需的时间互相独立,且都是整数分钟,经统计,以往播出100次所需的时间(t)的情况如下:
每次随机播出,若将频率视为概率.
(Ⅰ)求恰好在第6分钟后开始播出第3号广告的概率;
(Ⅱ)用X表示至第4分钟末已完整播出广告的次数,求x的分布列及数学期望.
| 类别 | 1号广告 | 2号广告 | 3号广告 | 4号广告 |
| 广告次数 | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
(Ⅰ)求恰好在第6分钟后开始播出第3号广告的概率;
(Ⅱ)用X表示至第4分钟末已完整播出广告的次数,求x的分布列及数学期望.