题目内容

20．正方体ABCD-A1B1C1D1，P、Q、R、S四点分别为AB、BC1、DD1、AD的中点，求证：P、Q、R、S四点共面．

分析 连接AD1，RS，BC1，由R、S四点分别为DD1、AD的中点，可证RS∥AD1，又AD1∥BC1，从而可证RS∥BC1，即可得证P、Q、R、S四点共面．

解答 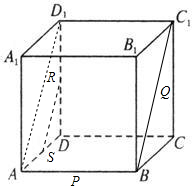证明：如图，连接AD1，RS，BC1，
∵ABCD-A1B1C1D1是正方体，
∴AD1∥BC1，
∵R、S四点分别为DD1、AD的中点，
∴RS∥AD1，
∴RS∥BC1，
∴P、Q、R、S四点共面．

点评 本题主要考查了线线平行的判定，考查了空间想象能力和推论论证能力，属于中档题．

练习册系列答案
相关题目
10．如图，在平面直角坐标系xOy中，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为，F1和F2，上顶点为B，BF2，延长线交椭圆于点A，△ABF的周长为8，且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0．
（Ⅰ）求椭圆的方程；
（Ⅱ）过点P（1，0）的直线l与椭圆C相交于M，N两点，点T（4，3），记直线TM，TN的斜率分别为k1，k2，当k1k2最大时，求直线l的方程．
11．已知函数f（x）=$\frac{1}{2}{x^2}$+（k-1）x-k+$\frac{3}{2}$，g（x）=xlnx．
（Ⅰ）若函数g（x）的图象在（1，0）处的切线l与函数f（x）的图象相切，求实数k的值；
（Ⅱ）当k=0时，证明：f（x）+g（x）＞0；
（Ⅲ）设h（x）=f（x）+g′（x），若h（x）有两个极值点x1，x2（x1≠x2），且h（x1）+h（x2）＜$\frac{7}{2}$，求实数k的取值范围．
8．化简（1+2${\;}^{-\frac{1}{16}}$）（1+2${\;}^{-\frac{1}{8}}$）（1+2${\;}^{-\frac{1}{4}}$）（1+2${\;}^{-\frac{1}{2}}$）得到的结果是（　　）
A．$\frac{1}{2}$（1-2${\;}^{-\frac{1}{16}}$）-1B．（1-2${\;}^{-\frac{1}{16}}$）-1C．1-2${\;}^{-\frac{1}{16}}$D．$\frac{1}{2}$（1-2${\;}^{-\frac{1}{16}}$）
15．棱长为1的正方体ABCD-A1B1C1D1中，点M，N，P分别为AB1，BC1，DD1的中点，给出下列结论：
①MN⊥AA1
②直线C1M与平面ABCD所成角的正弦值为$\frac{{\sqrt{5}}}{5}$
③MN⊥BP
④四面体B-DA1C1的体积为$\frac{1}{3}$
则正确结论的序号为①②③④．
5．用数学归纳法证明“当n为奇数时，xn+yn能被x+y整除”，在验证n=1正确后，归纳假设应写成（　　）
A．假设n=k（k∈N）时命题成立，即xk+yk能被x+y整除
B．假设n≥k（k∈N）时命题成立，即xk+yk能被x+y整除
C．假设n=2k+1（k∈N*）时命题成立，即x2k+1+y2k+1能被x+y整除
D．假设n=2k-1（k∈N*）时命题成立，即x2k-1+y2k-1能被x+y整除
12．已知A、B为抛物线C：y2=4x上的不同两点，F为抛物线C的焦点，若$\overrightarrow{FA}$=-4$\overrightarrow{FB}$，则直线AB的斜率为多少？
13．已知椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1、F2．其中F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且|MF1|=2a-$\frac{5}{3}$．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）若过点D（4，0）的直线l与C1交于不同的两点A、B，且A在DB之间，试求△AOD与BOD面积之比的取值范围．
14．已知数列{an}满足a1=2，an=$\frac{2（2n-1）}{n}$an-1（n≥2）．
（1）求数列{an}的通项公式；
（2）证明：a1+a2+…+an≤$\frac{2}{3}$（4n-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网