题目内容
1.已知椭圆$\frac{{x}^{2}}{4}$+y2=1,直线l:x-y+10=0,(Ⅰ)若M(x,y)为椭圆上的点,求x-y的最大值;
(Ⅱ)P为椭圆上的动点,求点P到直线l的距离的最大值.
分析 (Ⅰ)设出P的坐标,代入表达式利用三角函数的最值求解即可.
(Ⅱ)利用点到直线的距离公式,结合辅助角公式,即可求出到直线l:y=x+1的距离的最大值.
解答 解:(Ⅰ)设P(2cosθ,sinθ),θ∈R,
则x-y=2cosθ-sinθ=$\sqrt{5}$cos(θ+β),其中tanβ=2.
x-y的最大值为:$\sqrt{5}$.
(Ⅱ)P到直线l:x-y+10=0的距离d=$\frac{\left|2cosθ-sinθ+10\right|}{\sqrt{2}}$=$\frac{|\sqrt{5}cos(θ+β)+10|}{\sqrt{2}}$,其中tanβ=2
∴P到直线l:x-y+10=0的距离的最大值是$\frac{\sqrt{5}+10}{\sqrt{2}}$=$\frac{\sqrt{10}+10\sqrt{2}}{2}$.
点评 本题考查椭圆的参数方程,点到直线的距离公式的应用,考查学生的计算能力,是中档题.

练习册系列答案
相关题目
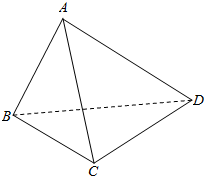 如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.
如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.