Question

（2008•武汉模拟）如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，BC∥AD，且∠BAD=90°，又PA⊥底面ABCD，BC=AB=PA=1，AD=2．
（1）求二面角P-CD-A的平面角正切值，
（2）求A到面PCD的距离．

Answer 1

分析：（1）在底面直角梯形ABCD中连接AC，利用余弦定理在三角形ACD中求出CD=

2

，从而得出AC⊥CD，所以AC为PC在平面ABCD内的射影，得CD⊥PC，因此∠PCA是二面角P-CD-A的平面角，最后在三角形PAC中求出此角的正弦，从而得出二面角P-CD-A的平面角正切值；
（2）过A作AH⊥PC于H，则AH⊥PC，故AH为A点到平面PCD之距离，在△PAC中，求得PA=1，AC=

2

，PC=

3

，从而得出
AH=

1× 2

3

=

6

3

，故A点到平面PCD的距离为

6

3

．

解答：解：（1）四棱锥P-ABCD中，底面ABCD是直角梯形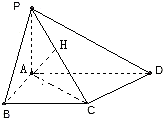
且BC∥DA，∠BAC=90°
连接AC，而AB=CB=1，则AC=

2

又因为AD=2，∠CAD=45°
由余弦定理可得CD=

2

，故AC⊥CD
∵PA⊥平面ABCD
∴AC为PC在平面ABCD内的射影
∴CD⊥PC
∴∠PCA是二面角P-CD-A的平面角
又PA=1，AC=

2

，所以PC=

3

，故sin∠PCA=

3

3

所以二面角P-CD-A的平面角的正切值等于

2

2

（2）由（1）可知DC⊥平面PAC
∴平面PAC⊥平面PCD
过A作AH⊥PC于H，则AH⊥PC，故AH为A点到平面PCD之距离
在△PAC中，PA=1，AC=

2

，PC=

3

∴AH=

1× 2

3

=

6

3

故A点到平面PCD的距离为

6

3

点评：本题考查了立体几何中的二面角的计算，属于中档题．在计算点到平面的距离时，注意要充分利用线面垂直和面面垂直的性质与判定．