题目内容
已知P为平行四边形ABCD所在平面外一点,E∈PB,F∈AC,且
=
,求证:EF∥平面PCD.
| PE |
| EB |
| CF |
| FA |
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:根据面面平行的性质定理证明平面EGF∥平面PCD,即可得到结论.
解答:
证明:如图所示,在BC上取一点G,使CG:GB=PE:EB,则GE∥PC,
∵
=
,
∴
=
,即CF∥CD,
∵GF?平面PCD,CD?平面PCD,
∴FG∥平面PCD,
同理EG∥平面PCD,
∵EG∩GF=G,
∴平面EGF∥平面PCD,
∵EF?平面EGF,
∴EF∥平面PCD.
∵
| PE |
| EB |
| CF |
| FA |
∴
| CF |
| FA |
| CG |
| GB |

∵GF?平面PCD,CD?平面PCD,
∴FG∥平面PCD,
同理EG∥平面PCD,
∵EG∩GF=G,
∴平面EGF∥平面PCD,
∵EF?平面EGF,
∴EF∥平面PCD.
点评:本题考查线面平行、面面平行的判定和性质定理的应用,考查学生分析解决问题的能力,属于基本知识的考查,属于中档题.

练习册系列答案
相关题目
黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
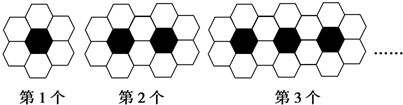
则第n个图案中的白色地面砖有( )

则第n个图案中的白色地面砖有( )
| A、4n-2块 |
| B、4n+2块 |
| C、3n+3块 |
| D、3n-3块 |