题目内容
【题目】已知边长为![]() 的正
的正![]() 的顶点
的顶点![]() 在平面
在平面![]() 内,顶点
内,顶点![]() ,
,![]() 在平面
在平面![]() 外的同一侧,点
外的同一侧,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 在平面
在平面![]() 内的投影,设
内的投影,设![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .若
.若![]() 是以角
是以角![]() 为直角的直角三角形,则
为直角的直角三角形,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
【解析】分析:由题意找出线面角,设BB′=a,CC′=b,可得ab=2,然后由a的变化得到A′B′的变化范围,从而求得tanφ的范围.
详解:如图,
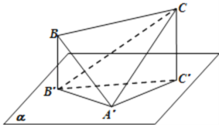
由CC′⊥α,A′B′α,得A′B′⊥CC′,
又A′B′⊥A′C′,且A′C′∩CC′=C′,
∴A′B′⊥面A′C′C,则φ=∠B′CA′,
设BB′=a,CC′=b,则A′B′2=4﹣a2,A′C′2=4﹣b2,
设B′C′=c,
则有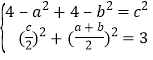 ,整理得:ab=2.
,整理得:ab=2.
∵|BB′|≤|CC′|,∴a≤b,
tanφ=![]() ,
,
在三角形BB′A′中,∵斜边A′B为定值2,
∴当a最大为![]() 时,A′B′取最小值
时,A′B′取最小值![]() ,tanφ的最小值为
,tanφ的最小值为![]() .
.
当a减小时,tanφ增大,
若a≤1,则b≥2,在Rt△A′CC′中出现直角边大于等于斜边,矛盾,
∴a>1,此时A′B′<![]() ,即tanφ
,即tanφ![]() .
.
∴tanφ的范围为![]() .即
.即![]() 的最小值为
的最小值为![]()
故答案为:![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某制造商![]() 月生产了一批乒乓球,随机抽样
月生产了一批乒乓球,随机抽样![]() 个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
分组 | 频数 | 频率 |
| 10 | |
| 20 | |
| 50 | |
| 20 | |
合计 | 100 |

(1)请在上表中补充完成频率分布表(结果保留两位小数),并在上图中画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).