Question

【题目】已知椭圆C： 过点 ，左右焦点为F1（﹣c，0），F2（c，0），且椭圆C关于直线x=c对称的图形过坐标原点．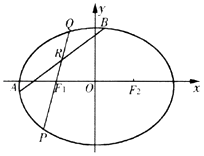

（I）求椭圆C方程；
（II）圆D： 与椭圆C交于A，B两点，R为线段AB上任一点，直线F1R交椭圆C于P，Q两点，若AB为圆D的直径，且直线F1R的斜率大于1，求|PF1||QF1|的取值范围．

Answer 1

【答案】解：（Ⅰ）∵椭圆C过点 ，
∴ ，①
∵椭圆C关于直线x=c对称的图形过坐标原点，∴a=2c，
∵a2=b2+c2 ， ∴ ，②
由①②得a2=4，b2=3，
∴椭圆C的方程为 ．…
（Ⅱ）因为AB为圆D的直径，所以点D： 为线段AB的中点，
设A（x1 ， y1），B（x2 ， y2），则， ，又 ，
所以 ，则（x1﹣x2）﹣（y1﹣y2）=0，故 ，
则直线AB的方程为 ，即 ，…
代入椭圆C的方程并整理得 ，则 ，
故直线F1R的斜率 ．
设F1R：y=k（x+1），由 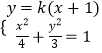，得（3+4k2）x2+8k2x+4k2﹣12=0，
设P（x3 ， y3），Q（x4 ， y4），则有 ， ．
又 ， ，…
所以|PF1||QF1|=（1+k2）|x3x4+（x3+x4）+1|= ，
因为 ，所以 ，
即|PF1||QF1|的取值范围是 ．
【解析】（I）将点代入椭圆方程，由函数的对称性求得a=2c，即可求得椭圆的标准方程；（II）由圆D，求得圆心坐标，利用点差法，求得直线AB的方程，代入椭圆方程，求得A，B点坐标，求得F1R的斜率的取值范围，则设F1R的方程y=k（x+1），代入椭圆方程，由韦达定理及 ， ，即可求得|PF1||QF1|的取值范围．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：，焦点在y轴：才能正确解答此题．