题目内容
1．已知a＞0，a≠1，求使关于x的方程$1o{g_{\sqrt{a}}}（x-2ka）=1o{g_a}（{x^2}-{a^2}）$有解时k的取值范围．分析 由题意把原方程化为$\left\{\begin{array}{l}{（x-2ak）^{2}={x}^{2}-{a}^{2}，（1）}\\{x-2ak＞0，（2）}\\{{x}^{2}-{a}^{2}＞0，（3）}\end{array}\right.$，进一步得到$\left\{\begin{array}{l}{（x-2ak）^{2}={x}^{2}-{a}^{2}，（1）}\\{x-2ak＞0，（2）}\end{array}\right.$，由（1）求得x，代入（2）转化为k的不等式求解．
解答 解：由$1o{g_{\sqrt{a}}}（x-2ka）=1o{g_a}（{x^2}-{a^2}）$，得
$\left\{\begin{array}{l}{（x-2ak）^{2}={x}^{2}-{a}^{2}，（1）}\\{x-2ak＞0，（2）}\\{{x}^{2}-{a}^{2}＞0，（3）}\end{array}\right.$当（1），（2）同时成立时，（3）显然成立，
因此只需解$\left\{\begin{array}{l}{（x-2ak）^{2}={x}^{2}-{a}^{2}，（1）}\\{x-2ak＞0，（2）}\end{array}\right.$
由（1）得4kx=a（1+4k2），（4）
当k=0时，由a＞0知（4）无解，因而原方程无解；
当k≠0时，（4）的解是x=$\frac{a（1+4{k}^{2}）}{4k}$，（5）
把（5）代入（2），得$\frac{（1+4{k}^{2}）}{4k}＞2k$．
解得：k＜-$\frac{1}{2}$或0＜k＜$\frac{1}{2}$．
综上，k的取值范围是（-∞，-$\frac{1}{2}$）∪（0，$\frac{1}{2}$）．
点评 本题主要考查函数的零点与方程根的关系、对数函数图象与性质的综合应用、不等式的解法等基础知识，考查运算求解能力，考查方程思想、化归与转化思想．属于中档题．
能考试期末冲刺卷系列答案| A． | （3，5） | B． | （-∞，2）∪（2，3） | C． | （2，3） | D． | （-∞，2）∪（3，5） |
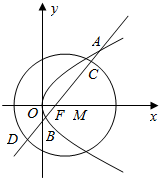如图，抛物线C1：y2=2px（p＞0）和圆C2：（x-1）2+y2=r2（r＞0），M为圆C2的圆心，过抛物线C1的焦点F的直线y=k（x-$\frac{p}{2}$）与C1交于A，B两点，与圆C2交与C，D两点（点C在A，B之间）且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$．
已知函数f（x）=sinx+$\sqrt{3}$cosx．| A． | r≤2 | B． | r＜2 | C． | r＜$\frac{1}{2}$ | D． | r≤$\frac{1}{2}$ |