题目内容
13. 如图,在四面体P-ABC中,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,二面角C-AB-P的正切值为$\sqrt{5}$.
如图,在四面体P-ABC中,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,二面角C-AB-P的正切值为$\sqrt{5}$.(Ⅰ)求证:PA⊥BC;
(Ⅱ)求异面直线PC与AB所成角的余弦值.
分析 (Ⅰ)在平面ABC内,作HD∥AB,根据已知条件可说明HB,HD,HP三直线两两垂直,从而可分别以这三直线为x,y,z轴,建立空间直角坐标系,根据条件可求出图中各点的坐标,然后求$\overrightarrow{PA}•\overrightarrow{BC}=0$即可;
(Ⅱ)求向量$\overrightarrow{PC},\overrightarrow{AB}$的坐标,可设异面直线PC与AB所成角为θ,从而根据cosθ=$|cos<\overrightarrow{PC},\overrightarrow{AB}>|$=$\frac{|\overrightarrow{PC}•\overrightarrow{AB}|}{|\overrightarrow{PC}||\overrightarrow{AB}|}$即可求得异面直线PC与AB所成角的余弦值.
解答 解:(Ⅰ)证明:过H作HD∥AB,PH⊥底面ABC,AB?平面ABC;
∴PH⊥AB,即AB⊥PH;
又AB⊥BP,BP∩PH=P;
∴AB⊥平面PBH;
∴AB⊥BH,∴HD⊥BH;
∴HB,HD,HP三直线两两垂直,分别以这三条直线为x,y,z轴,建立如图所示空间直角坐标系,则根据条件: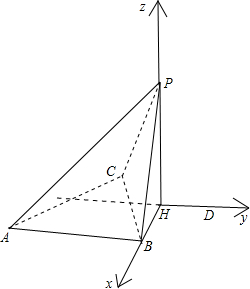
H(0,0,0),A($\frac{\sqrt{3}}{3},-1,0$),B($\frac{\sqrt{3}}{3}$,0,0),C($-\frac{\sqrt{3}}{6},-\frac{1}{2},0$);
∵AB⊥BH,AB⊥BP;
∴∠PBH为二面角C-AB-P的平面角,∴tan∠PBH=$\frac{PH}{BH}=\frac{PH}{\frac{\sqrt{3}}{3}}=\sqrt{5}$;
∴PH=$\frac{\sqrt{15}}{3}$,∴$P(0,0,\frac{\sqrt{15}}{3})$;
∴$\overrightarrow{PA}$=($\frac{\sqrt{3}}{3},-1,-\frac{\sqrt{15}}{3}$),$\overrightarrow{BC}$=($-\frac{\sqrt{3}}{2}$,$-\frac{1}{2},0$);
∴$\overrightarrow{PA}•\overrightarrow{BC}=0$;
∴$\overrightarrow{PA}⊥\overrightarrow{BC}$;
∴PA⊥BC;
(Ⅱ)$\overrightarrow{PC}=(-\frac{\sqrt{3}}{6},-\frac{1}{2},-\frac{\sqrt{15}}{3})$,$\overrightarrow{AB}=(0,1,0)$;
设异面直线PC与AB所成角为θ,则:
cosθ=$|cos<\overrightarrow{PC},\overrightarrow{AB}>|$=$\frac{\frac{1}{2}}{\sqrt{2}}=\frac{\sqrt{2}}{4}$;
异面直线PC与AB所成角的余弦值为$\frac{\sqrt{2}}{4}$.
点评 考查线面垂直的性质,线面垂直的判定定理,通过建立空间直角坐标系,利用空间向量证明异面直线垂直、异面直线所成角的方法,二面角的平面角的定义,等边三角形的中线也是高线,以及两非零向量垂直的充要条件,向量夹角余弦的坐标公式.

| A. | “若平面上两直线互相垂直,则这两条直线的斜率之积为-1”为真命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“?x0∈R,${2}^{{x}_{0}}$≤0” | |
| C. | 命题“幂函数y=${x}^{\frac{1}{3}}$的定义域为R”是假命题 | |
| D. | 在△ABC中,“A>B”是“sinA>sinB”的充分不必要条件 |
(1)cos(α+β);
(2)cos(α-β).
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
 如图,在多面体ABCDE中,面ABED为梯形且∠BAD=∠EDA=$\frac{π}{2}$,F为CE的中点,AC=AD=CD=DE=AF=2,AB=1.
如图,在多面体ABCDE中,面ABED为梯形且∠BAD=∠EDA=$\frac{π}{2}$,F为CE的中点,AC=AD=CD=DE=AF=2,AB=1. 如图,已知四棱锥P-ABCD的底面是菱形,对角线AC,BD交于点O,OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).
如图,已知四棱锥P-ABCD的底面是菱形,对角线AC,BD交于点O,OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).