题目内容
4. 如图,在多面体ABCDE中,面ABED为梯形且∠BAD=∠EDA=$\frac{π}{2}$,F为CE的中点,AC=AD=CD=DE=AF=2,AB=1.
如图,在多面体ABCDE中,面ABED为梯形且∠BAD=∠EDA=$\frac{π}{2}$,F为CE的中点,AC=AD=CD=DE=AF=2,AB=1.(1)求证:DF⊥BC;
(2)求平面BCE与平面ACD所成锐二面角的余弦值.
分析 (1)取CD的中点O,连接AO,FO,则AO⊥CD,证明AO⊥OF,可得AO⊥平面CDE,建立如图所示的坐标系,利用向量的方法证明DF⊥BC;
(2)确定平面BCE与平面ACD的法向量,即可求平面BCE与平面ACD所成锐二面角的余弦值.
解答 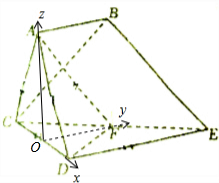 (1)证明:取CD的中点O,连接AO,FO,则AO⊥CD
(1)证明:取CD的中点O,连接AO,FO,则AO⊥CD
由题意,AO=$\sqrt{3}$,OF=1,
∵AF=2,
∴AO⊥OF,
∵CD∩OF=O,
∴AO⊥平面CDE,
建立如图所示的坐标系,则D(1,0,0),F(0,1,0),B(0,1,$\sqrt{3}$),C(-1,0,0),
∴$\overrightarrow{DF}$=(-1,1,0),$\overrightarrow{BC}$=(-1,-1,-$\sqrt{3}$),
∴$\overrightarrow{DF}•\overrightarrow{BC}$=0,
∴DF⊥BC;
(2)解:由(1)可得DF⊥平面CBE
∴平面CBE的法向量为$\overrightarrow{DF}$=(-1,1,0),
∵平面ACD的法向量为(0,1,0),
∴平面BCE与平面ACD所成锐二面角的余弦值为$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 解决立体几何中的线、面的位置关系或度量关系,常用的方法是通过建立空间直角坐标系,转化为向量的问题来解决.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
4. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )
 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )| A. | $\frac{{\sqrt{3}π}}{4}$ | B. | $\frac{{\sqrt{3}π}}{2}$ | C. | $\sqrt{3}π$ | D. | 3π |
14.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $8+2\sqrt{2}$ | B. | $8+4\sqrt{2}$ | C. | $12+2\sqrt{2}$ | D. | $12+4\sqrt{2}$ |
 如图,在四面体P-ABC中,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,二面角C-AB-P的正切值为$\sqrt{5}$.
如图,在四面体P-ABC中,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,二面角C-AB-P的正切值为$\sqrt{5}$.