题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,其中
,其中![]() 是自然对数的底数,求
是自然对数的底数,求![]() 的值:
的值:
(Ⅱ)若函数![]() 是
是![]() 内的减函数,求正数
内的减函数,求正数![]() 的取值范围;
的取值范围;
(Ⅲ)若方程![]() 无实数根,求实数
无实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)1;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]() .
.
【解析】
(Ⅰ)先对函数求导,然后根据导数的几何意义及已知切线方程即可求解;
(Ⅱ)结合导数与单调性的关系可转化为![]() 在
在![]() 内恒成立,结合函数的性质可求;
内恒成立,结合函数的性质可求;
(Ⅲ)结合导数及函数的性质,进行合理的转化后结合导数可求.
解:(Ⅰ)已知![]() ,
,![]()
![]() ,
,
由曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
可得![]() ,得
,得![]() ,
,
则![]() ,
,![]() ,
,
解得:![]() .
.
(Ⅱ)若函数![]() 是
是![]() 内的减函数,
内的减函数,
则![]() 在
在![]() 内恒成立,
内恒成立,
令![]() ,则
,则![]() ,
,
①![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
②若![]() ,当
,当 ,
,![]() ,
,![]() 单调递增,
单调递增,
所以![]() ,
,
③![]() 时,
时,![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,
综上,![]() 时,满足题意;
时,满足题意;
(Ⅲ)由![]() 可得
可得![]() ,
,
若![]() ,则
,则![]() 是方程
是方程![]() 的根,故
的根,故![]() ,
,
若![]() ,则
,则![]() 无实根,
无实根,
若![]() ,令
,令![]() ,则
,则![]() ,
,
方程![]() 可化为
可化为![]() 即
即![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() ,
,
若![]() 没有实根,则
没有实根,则![]() ,
,
解得:![]() 或
或![]() ,
,
综上:![]() 或
或![]() .
.

【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;
②A品牌三种车型总销量环比增长率可能大于14.70%;
③B品牌三款车型总销量环比增长率可能为正;
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
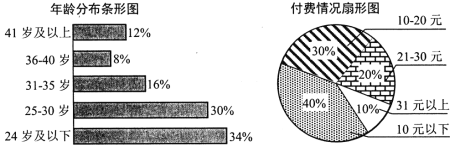
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
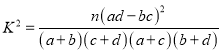 .
.