题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() ,
,![]() 两点,若点
两点,若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据离心率得到![]() 之间的关系,把点
之间的关系,把点![]() 代入椭圆
代入椭圆![]() 方程即可求解;
方程即可求解;
(2)分直线![]() 的斜率存在和不存在两种情况进行证明:当
的斜率存在和不存在两种情况进行证明:当![]() 不垂直于
不垂直于![]() 轴时,设直线
轴时,设直线![]() :
:![]() 与椭圆
与椭圆![]() 方程联立,设
方程联立,设![]() ,
,![]() ,则
,则![]() ,利用韦达定理进行证明即可;当
,利用韦达定理进行证明即可;当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() 即
即![]() 轴,过
轴,过![]() .
.
(1)由题意,![]() ,∴
,∴![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ,
,
把点![]() 代入椭圆
代入椭圆![]() 的方程可得
的方程可得![]() ,
,
∴所求椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:当![]() 不垂直于
不垂直于![]() 轴时,设直线
轴时,设直线![]() :
:![]()
联立方程 ,可得
,可得![]() ,
,
由![]() 可得,
可得,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
由韦达定理可得,![]() ,
,
∴直线![]() 的方程为:
的方程为:![]() ,
,
令![]() ,
,![]()
![]()
![]()
 。
。
∴直线![]() 过定点
过定点![]() ,
,
当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() 即
即![]() 轴,过
轴,过![]() .
.
综上可知,直线![]() 过定点
过定点![]() .
.

【题目】新型冠状病毒肺炎![]() 疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.
疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.
日期代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数 | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染人数的变化趋势,小王同学分别用两种模型:①![]() ,②
,②![]() 对变量
对变量![]() 和
和![]() 的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差
的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差![]() ):经过计算得
):经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
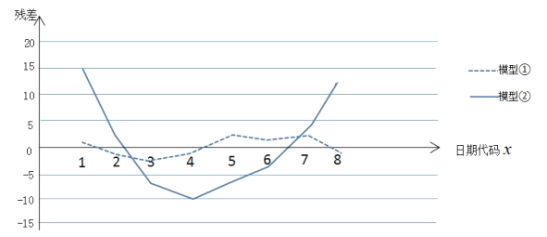
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由;
(2)根据(1)问选定的模型求出相应的回归方程(系数均保留一位小数);
(3)由于时差,该国截止第9天新型冠状病毒感染确诊的累计人数尚未公布.小王同学认为,如果防疫形势没有得到明显改善,在数据公布之前可以根据他在(2)问求出的回归方程来对感染人数作出预测,那么估计该地区第9天新型冠状病毒感染确诊的累计人数是多少.
附:回归直线的斜率和截距的最小二乘估计公式分别为: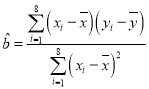 ,
,![]() .
.