题目内容
设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域.
(2)求f(x)在区间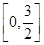 上的最大值.
上的最大值.
(1)求a的值及f(x)的定义域.
(2)求f(x)在区间
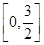 上的最大值.
上的最大值.解:∵f(1)=2,∴loga4=2(a>0,a≠1),
∴a=2.
由 ,得x∈(-1,3),
,得x∈(-1,3),
∴函数f(x)的定义域为 (-1,3).
(2)f(x)=log2(1+x)+log2(3-x)
=log2(1+x)(3-x)=log2[-(x-1)2+4],
∴当x∈(-1,1]时,f(x)是增函数;
当x∈(1,3)时,f(x)是减函数,
函数f(x)在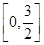 上的最大值是f(1)=log24=2.
上的最大值是f(1)=log24=2.
∴a=2.
由
 ,得x∈(-1,3),
,得x∈(-1,3),∴函数f(x)的定义域为 (-1,3).
(2)f(x)=log2(1+x)+log2(3-x)
=log2(1+x)(3-x)=log2[-(x-1)2+4],
∴当x∈(-1,1]时,f(x)是增函数;
当x∈(1,3)时,f(x)是减函数,
函数f(x)在
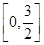 上的最大值是f(1)=log24=2.
上的最大值是f(1)=log24=2.
练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 ,则( )
,则( ) 的图象向左平移1个单位,再将位于
的图象向左平移1个单位,再将位于 轴下方的图象沿
轴下方的图象沿 的图象,若实数
的图象,若实数 满足
满足
 则
则 的值是( )
的值是( )



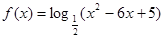 的单调递减区间是 .
的单调递减区间是 .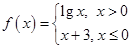 ,若
,若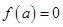 ,则实数
,则实数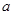 的值等于( )
的值等于( ) 

 或
或
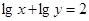 ,则
,则 +
+ 的最小值为( ).
的最小值为( ).

