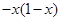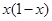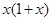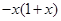题目内容
设函数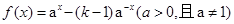 是定义域为
是定义域为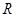 的奇函数.
的奇函数.
(1)求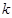 的值;
的值;
(2)若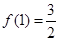 ,且
,且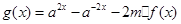 在
在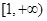 上的最小值为
上的最小值为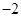 ,求
,求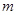 的值.
的值.
(3)若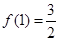 ,试讨论函数
,试讨论函数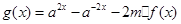 在
在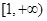 上零点的个数情况。
上零点的个数情况。
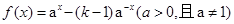 是定义域为
是定义域为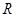 的奇函数.
的奇函数.(1)求
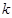 的值;
的值;(2)若
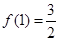 ,且
,且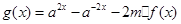 在
在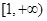 上的最小值为
上的最小值为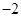 ,求
,求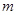 的值.
的值.(3)若
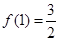 ,试讨论函数
,试讨论函数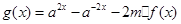 在
在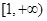 上零点的个数情况。
上零点的个数情况。(1) 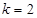 ;(2)
;(2)  (3) 当
(3) 当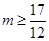 时
时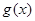 在
在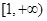 上有一个零点;当
上有一个零点;当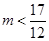 时
时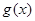 在
在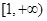 上无零点.
上无零点.
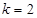 ;(2)
;(2)  (3) 当
(3) 当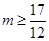 时
时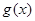 在
在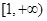 上有一个零点;当
上有一个零点;当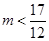 时
时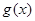 在
在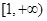 上无零点.
上无零点.试题分析:(1) 由奇函数的性质求
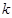 ,可用特殊值或用恒等式对应项系数相等,如果0在奇函数的定义域内,则一定有
,可用特殊值或用恒等式对应项系数相等,如果0在奇函数的定义域内,则一定有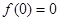 ,如果不在可任取定义域内两个相反数代入求
,如果不在可任取定义域内两个相反数代入求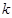 .
.(2)由
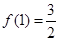 求出
求出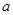 ,代入得
,代入得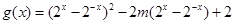 ,换元
,换元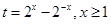 ,注意自变量的取值范围,每设出一个子母都要把它取的范围缩到最小以有利于解题, 所以得到
,注意自变量的取值范围,每设出一个子母都要把它取的范围缩到最小以有利于解题, 所以得到 得到一个新的函数
得到一个新的函数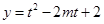 ,
, 利用二次函数函数单调性求最值方法得到
利用二次函数函数单调性求最值方法得到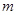 ,二次函数在区间上的最值在端点处或顶点处,遇到对称轴或区间含有待定的字母,则要按对称轴在不在区间内以及区间中点进行讨论.
,二次函数在区间上的最值在端点处或顶点处,遇到对称轴或区间含有待定的字母,则要按对称轴在不在区间内以及区间中点进行讨论.(3)由函数零点判定转化为二次方程根的判定,即
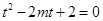 在
在 解个数情况,这个解起来比较麻烦,所以可以用函数单调性先来判定零点的个数,即
解个数情况,这个解起来比较麻烦,所以可以用函数单调性先来判定零点的个数,即 在
在 上为增函数,也就是在
上为增函数,也就是在 这个区间上是一一映射,
这个区间上是一一映射, 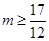 时的每个值方程
时的每个值方程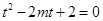 只有一个解.
只有一个解.试题解析:
(1)
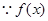 为
为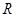 上的奇函数
上的奇函数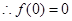 即
即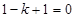
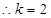
(2)由(1)知
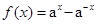
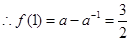 解得
解得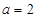 或
或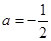 (舍)
(舍) 且
且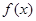 在
在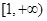 上递增
上递增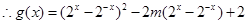
令
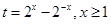 则
则
所以令
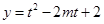 ,
, 且
且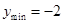
因为
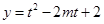 的对称轴为
的对称轴为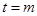
Ⅰ当
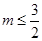 时
时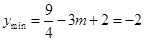
解得
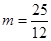 (舍)
(舍)Ⅱ当
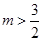 时
时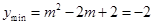
解得

综上:

(3)由(2)可得:
令
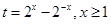 则
则
即求
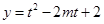 ,
, 零点个数情况
零点个数情况即求
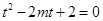 在
在 解个数情况
解个数情况由
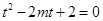 得
得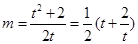 ,
,
所以
 在
在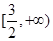 上为增函数
上为增函数当
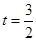 时
时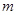 有最小值为
有最小值为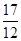
所以当
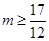 时
时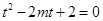 方程在
方程在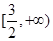 上有一根,即函数有一个零点
上有一根,即函数有一个零点当
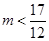 时
时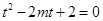 方程在
方程在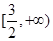 上无根,即函数无零点
上无根,即函数无零点综上所述:当
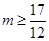 时
时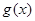 在
在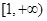 上有一个零点
上有一个零点当
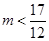 时
时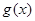 在
在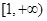 上无零点.
上无零点.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
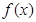 (
(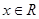 )是奇函数,函数
)是奇函数,函数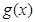 (
(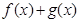 是奇函数
是奇函数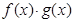 是奇函数
是奇函数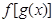 是奇函数
是奇函数 是奇函数
是奇函数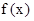 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且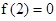 ,则方程
,则方程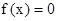 在区间(0,6)内解的个数的最小值是 .
在区间(0,6)内解的个数的最小值是 .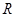 上的函数
上的函数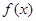 满足
满足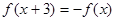 ,当
,当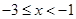 时,
时,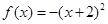 ,当
,当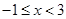 时,
时,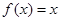 .则
.则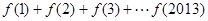 =( )
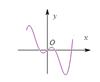
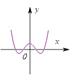
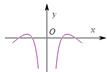
=( )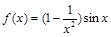 的图象大致为
的图象大致为 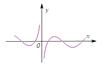
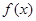 为定义在
为定义在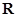 上的奇函数,当
上的奇函数,当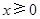 时,
时,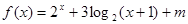 (
(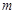 为常数),则
为常数),则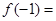 ( )
( )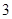
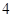
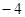
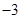
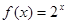 且
且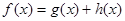 ,其中
,其中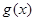 为奇函数,
为奇函数,  为偶函数,若不等式
为偶函数,若不等式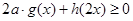 对任意
对任意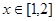 恒成立,则实数
恒成立,则实数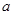 的取值范围是 .
的取值范围是 .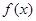 是定义在
是定义在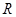 上的奇函数,当
上的奇函数,当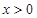 时,
时,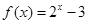 ,那么
,那么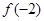 的值是( )
的值是( )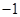
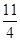
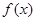 是奇函数,当
是奇函数,当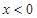 时,
时,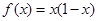 ,当
,当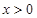 时,
时,